Model Representation I
신경망을 사용해서 어떻게 hypothesis function을 표현할 지 생각해보도록 하자. 매우 간단한 수준에서, 뉴런은 전기적 신호로 입력을 받아서 출력을 채널링하는 계산 유닛으로 생각할 수 있다. 모델의 개념으로 생각해보면 입력은 feature $x_1, \cdots x_n$이 되고, 출력은 hypothesis function의 결과가 된다. 모델에서 $x_0$ 입력 노드는 bias unit으로 불리기도 하는데, 이 노드는 항상 1의 값을 가진다. 신경망에서 분류처럼 똑같은 logistic function이고, sigmoid 활성화 함수라고도 불리는 $\frac {1}{1+e^{-\theta^{T}x}}$을 사용한다. 이 상황에서 세타 파라미터는 가중치라고도 불린다.
시각적으로 간단하게 표현하면 다음과 같다.
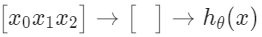
'입력 레이어'라고도 알려져 있는, 입력 노드$($layer 1$)$는 다른 노드$($layer 2$)$로 향하게 된다. 이 다른 노드는 hypothesis function의 최종 출력을 출력하는데, '출력 레이어'라고 불린다. 이 두 레이어 중간에 다른 레이어들도 존재하는데, 이들을 'hidden layer'라고 부른다. 이 예시에서는, 이 중간 혹은 'hidden' 레이어 노드 $a_{0}^{2} \cdots a_{n}^{2}$로 라벨링하고 'activation unit'이라고 부른다.
만약 하나의 hidden layer를 가지고 있다면 다음과 같은 형태를 가지게 된다.
각 'activation' 노드들의 값은 다음과 같이 얻게 된다.
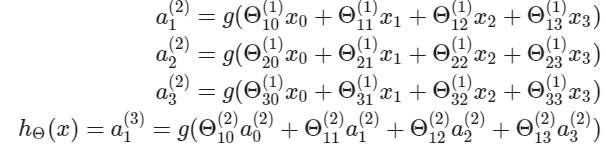
activation node는 $3 \times 4$ 크기의 행렬을 이용해서 계산된다. 파라미터의 각 행을 입력에 적용해서 하나의 activation node에 대한 값을 얻는다. hypothesis 출력은 노드의 두 번째 레이어에 대한 가중치를 포함하는 또 다른 매개변수 행렬 $\theta^{2}$로 곱해진 activation node 값의 합에 적용된 logistic 함수이다.
각 레이어는 각자의 가중치 행렬인 $\theta^{(j)}$을 갖는다. 이 가중치 행렬의 차원은 다음과 같이 결정된다.
layer j에서 네트워크가 $s_j$ 유닛과 layer j+1에서 $s_{j+1}$ 유닛을 가지면 $\theta^{j}$의 차원은 $s_{j+1} \times (s_{j} + 1)$을 가진다.
1이 더해진 이유는 $\theta^{(j)}$의 bias node인 $x_{0}$과 $\theta_{0}^{(j)}$의 추가로 온 것이다. 즉, 출력 노드에는 bias node를 포함되지 않지만, 입력 노드에는 포함된다. 다음의 그림은 model 표현을 요약하고 있다.

예를 들어, layer 1이 2개의 입력 노드를 갖고, layer 2가 4개의 activation node를 가진다고 해보자. $\theta^{(1)}$의 차원은 $4 \times 3$이 된다. 여기서 $s_j = 2$이고 $s_{j+1}=4$이다. 그래서 $s_{j+1} \times (s_j + 1) = 4 \times 3$이 된다.
Model Representation II
다음은 신경망의 예시이다.
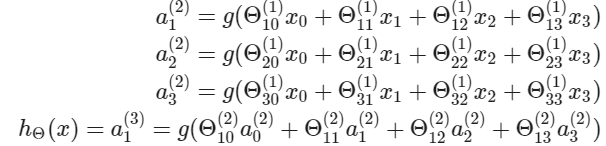
이 섹션에서는 위 함수의 벡터화된 구현을 해보도록 하겠다. $g$ 함수의 안에 있는 파라미터를 포함하는 새로운 변수 $z_{k}^{(j)}$을 정의하도록 하겠다. 이전의 예시에서 모든 파라미터를 변수 $z$로 바꾸면 다음을 얻게 된다.
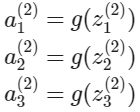
다른 말로 하면, layer $j=2$와 노드 $k$에 대해 변수 $z$는 다음과 같다.
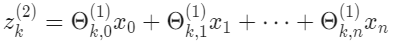
$x$와 $z^{j}$의 벡터 표현은 다음과 같다.
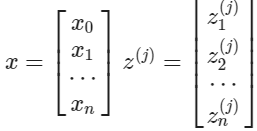
$x = a^{(1)}$으로 설정하면, 방정식을 다음과 같이 바꿔 쓸 수 있다.
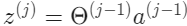
행렬 $\theta^{(j-1)}$과 차원 $s_j \times (n+1)$$($여기서 $s_j$는 activation node의 수$)$을 높이 $(n+1)$인 벡터 $a^{(j-1)}$과 곱한다. 이것은 높이가 $s_j$인 벡터 $z^{(j)}$를 준다. 이제 layer $j$에 대한 activation node의 벡터를 다음과 같이 얻을 수 있다.
$a^{(j)} = g(z^{(j)})$
여기서 함수 $g$는 벡터 $z^{(j)}$에 element-wise하게 적용될 수 있다. $a^{(j)}$를 계산한 다음에 layer $j$에 bias unit을 더할 수 있다. 이것은 원소 $a_{0}^{(j)}$가 되고, 1과 같은 값을 가지게 된다. 최종 hypothesis를 게사하기 위해, 다른 $z$벡터부터 계산해야 한다.
$z^{(j+1)} = \theta^{(j)}a^{(j)}$
방금 얻은 모든 activation node의 값을 $\theta^{(j-1)}$ 다음 세타 행렬에 곱하여 최종 벡터 $z$를 얻는다. 이 마지막 세타 행렬 $\theta^{(j)}$는 오직 하나의 행을 가질 것이고, 이는 하나의 열 $a^{(j)}$에 의해 곱해져서 결과적으로 하나의 숫자를 갖게 된다. 최종적인 결과는 다음과 같다.
$h_{\theta}(x) = a^{(j+1)} = g(z^{(j+1)})$
layer $j$와 layer $j+1$ 사이의 이 마지막 단계에서 logistic regression에서 했던 것과 정확히 같은 일을 하고 있다. 이러한 모든 중간 레이어들을 신경망에 추가하는 것은 더 세련되고 흥미로운 출력을 하고, 복잡한 비선형 hypothesis를 가능하게 해준다.
'Lecture 🧑🏫 > Coursera' 카테고리의 다른 글
| [Machine Learning] Backpropagation in Practice (0) | 2023.03.27 |
|---|---|
| [Machine Learning] Cost Function & Backpropagation (0) | 2023.03.26 |
| [Machine Learning] Solving the Problem of Overfitting (2) | 2023.03.20 |
| [Machine Learning] Multiclass Classification (0) | 2023.03.15 |
| [Machine Learning] Classification & Representation (0) | 2023.03.15 |
