Diagnosing Bias vs Variance
이 섹션에서는 polynomial d와 hypothesis의 underfitting 혹은 overfitting의 관계에 대해서 조사하였다.
- 잘못된 예측에 공헌하는 bias와 variance를 구분하였다.
- 높은 bias는 underfitting을 야기하고, 높은 variance는 overfitting을 야기한다. 따라서 이 둘 간의 황금 평균을 찾아야 할 필요가 있다.
polynomial의 degree d를 증가시킬 수록 training error는 감소하는 경향이 있다. 동시간대에 cross validation error는 일정 포인트까지는 감소하는 경향이 있고, 그 다음에는 d값이 오름에 따라 상승하면서, convex curve를 만들어 낸다 $($최솟값 또는 최댓값이 하나인 커브$)$.
- High bias$($underfitting$)$: $J_{train}(\theta)$와 $J_{CV}(\theta)$ 둘 다 높다. 또한 $J_{CV}(\theta) \approx J_{train}(\theta)$
- High variance$($overfitting$)$: $J_{train}(\theta)$는 낮고, $J_{CV}(\theta)$는 $J_{train}(\theta)$ 보다 훨씬 크다.
이것을 요약한 그림은 다음과 같다.

Regularization and Bias/Variance
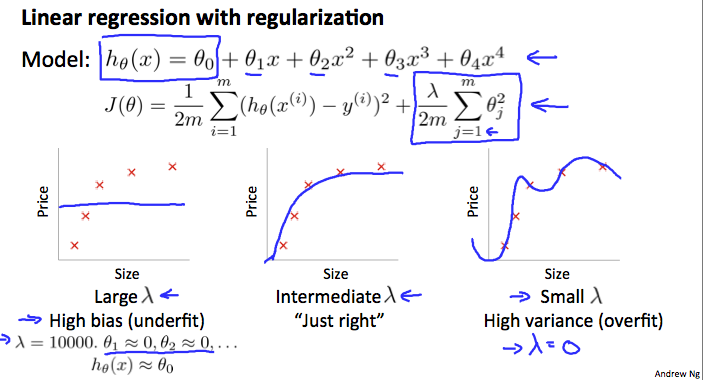
위의 그림에서처럼 $\lambda$가 증가함에 따라 직선에 가깝게 fit되는 것을 알 수 있다. 반대로 $\lambda$가 0에 근접함에 따라 데이터에 overfit되는 경향이 있다. 어떻게 하면 올바른 파라미터 $\lambda$를 얻을 수 있을까? 그러기 위해서는 모델과 정규화 항 $\lambda$를 다음과 같이 선택해야 한다.
- lambda 리스트를 생성한다.
- 서로 다른 degree 혹은 variant를 사용해서 모델의 세트를 만든다.
- $\lambda$를 반복하고 각 $\lambda$에 대해 모든 모델을 거쳐 일부 $\theta$를 학습한다.
- 정규화 또는 $\lambda = 0$ 없이 $J_{CV}(\theta)$에서 학습된 $\theta$를 사용해서 cross validation 오차를 계산한다.
- cross validation set에서 가장 낮은 오차를 만들어내는 콤보를 선택한다.
- 최고의 콤보 $\theta$와 $\lambda$를 $J_{test}(\theta)$에 적용해서 문제의 좋은 일반화를 본다.
Learning Curves
매우 적은 수의 데이터 포인트$($예: 1, 2 또는 3$)$에서 알고리즘을 교육하면 해당 포인트 수에 정확히 닿는 2차 곡선을 항상 찾을 수 있기 때문에 쉽게 오차가 0이 된다. 따라서:
- training set이 커질수록 2차 함수에 대한 오차는 커진다.
- 오차값은 특정 m 또는 training set 크기가 지난 후에 안정에 이른다.
Experiencing high bias
- Low training set size: $J_{train}(\theta)$는 낮고, $J_{CV}(\theta)$는 높아진다.
- Large training set size: $J_{train{(\theta)$와 $J_{CV}(\theta)$는 둘 다 $J_{train}(\theta) \approx J_{CV}(\theta)$ 정도에서 높다.
만약 학습 알고리즘이 high bias를 겪는다면, 더 많은 training data를 가지는 것이 별 도움이 되지 않는다.

Experiencing high variance
- Low training set size: $J_{train}(\theta)$는 낮고 $J_{CV}(\theta)$는 높다.
- Large training set size: $J_{train}(\theta)$는 training set size와 함께 증가하고 $J_{CV}(\theta)$는 레벨링 오프 없이 계속해서 감소한다. 또한 $J_{train}(\theta) < J_{CV}(\theta)$이지만, 둘 간의 차이는 분명히 존재한다.
만약 학습 알고리즘이 high variance를 겪는다면 더 많은 training data를 가지는 것이 도움이 된다.
Deciding What to do Next Revisited
선택 프로세스는 다음과 같이 쪼개진다. 우선 high variance의 경우 이런 방법들을 추천한다.
- 더 많은 training example 가지기
- feature set를 줄이기
- $\lambda$를 증가시키기
반대로 high bias의 경우 이런 방법들을 추천한다.
- feature 추가하기
- polynomial feature 추가하기
- $\lambda$를 감소시키기
신경망 네트워크 진단
- 적은 파라미터를 사용하는 신경망 네트워크는 underfitting될 가능성이 있다. 하지만 계산 비용은 적다.
- 더 많은 파라미터를 사용하는 큰 신경망 네트워크는 overfitting될 가능성이 있다. 하지만 계산 비용은 크다. 이 경우에는 정규화를 사용$(\lambda$값 증가시키기$)$하여 overfitting을 해결할 수 있다.
하나의 hidden layer을 사용하는 것이 좋은 시작 기본값이다. cross validation set를 사용해서 여러 개의 hidden layer에서 신경망 네트워크를 학습시킬 수 있다. 그 중에 가장 좋은 성능을 보여주는 모델을 선택하면 된다.
모델 복잡도 효과
- lower-order polynomial$($낮은 모델 복잡도$)$은 high bais와 low variance를 가진다. 이 경우에 모델은 일관적으로 좋지 않은 성능을 보여준다.
- higher-order polynomial$($높은 모델 복잡도$)$은 training data에는 잘 적용되지만, test data에서는 좋지 않은 성능을 보여준다. 이는 training data에 대해 low bias를 가지고 high variance를 가지게 된다.
- 실제로, 잘 일반화할 수 있지만 데이터에 합리적으로 잘 맞는 중간 어딘가에 있는 모델을 선택해야 한다.
'Lecture 🧑🏫 > Coursera' 카테고리의 다른 글
| [Machine Learning] Machine Learning Algorithm Application (0) | 2023.03.28 |
|---|---|
| [Machine Learning] Evaluating a Learning Algorithm (0) | 2023.03.27 |
| [Machine Learning] Backpropagation in Practice (0) | 2023.03.27 |
| [Machine Learning] Cost Function & Backpropagation (0) | 2023.03.26 |
| [Machine Learning] Neural Networks (0) | 2023.03.20 |
Diagnosing Bias vs Variance
이 섹션에서는 polynomial d와 hypothesis의 underfitting 혹은 overfitting의 관계에 대해서 조사하였다.
- 잘못된 예측에 공헌하는 bias와 variance를 구분하였다.
- 높은 bias는 underfitting을 야기하고, 높은 variance는 overfitting을 야기한다. 따라서 이 둘 간의 황금 평균을 찾아야 할 필요가 있다.
polynomial의 degree d를 증가시킬 수록 training error는 감소하는 경향이 있다. 동시간대에 cross validation error는 일정 포인트까지는 감소하는 경향이 있고, 그 다음에는 d값이 오름에 따라 상승하면서, convex curve를 만들어 낸다 ((최솟값 또는 최댓값이 하나인 커브)).
- High bias((underfitting)): Jtrain(θ)Jtrain(θ)와 JCV(θ)JCV(θ) 둘 다 높다. 또한 JCV(θ)≈Jtrain(θ)JCV(θ)≈Jtrain(θ)
- High variance((overfitting)): Jtrain(θ)Jtrain(θ)는 낮고, JCV(θ)JCV(θ)는 Jtrain(θ)Jtrain(θ) 보다 훨씬 크다.
이것을 요약한 그림은 다음과 같다.

Regularization and Bias/Variance

위의 그림에서처럼 λλ가 증가함에 따라 직선에 가깝게 fit되는 것을 알 수 있다. 반대로 λλ가 0에 근접함에 따라 데이터에 overfit되는 경향이 있다. 어떻게 하면 올바른 파라미터 λλ를 얻을 수 있을까? 그러기 위해서는 모델과 정규화 항 λλ를 다음과 같이 선택해야 한다.
- lambda 리스트를 생성한다.
- 서로 다른 degree 혹은 variant를 사용해서 모델의 세트를 만든다.
- λλ를 반복하고 각 λλ에 대해 모든 모델을 거쳐 일부 θθ를 학습한다.
- 정규화 또는 λ=0λ=0 없이 JCV(θ)JCV(θ)에서 학습된 θθ를 사용해서 cross validation 오차를 계산한다.
- cross validation set에서 가장 낮은 오차를 만들어내는 콤보를 선택한다.
- 최고의 콤보 θθ와 λλ를 Jtest(θ)Jtest(θ)에 적용해서 문제의 좋은 일반화를 본다.
Learning Curves
매우 적은 수의 데이터 포인트((예: 1, 2 또는 3))에서 알고리즘을 교육하면 해당 포인트 수에 정확히 닿는 2차 곡선을 항상 찾을 수 있기 때문에 쉽게 오차가 0이 된다. 따라서:
- training set이 커질수록 2차 함수에 대한 오차는 커진다.
- 오차값은 특정 m 또는 training set 크기가 지난 후에 안정에 이른다.
Experiencing high bias
- Low training set size: Jtrain(θ)Jtrain(θ)는 낮고, JCV(θ)JCV(θ)는 높아진다.
- Large training set size: $J_{train{(\theta)와J_{CV}(\theta)는둘다J_{train}(\theta) \approx J_{CV}(\theta)$ 정도에서 높다.
만약 학습 알고리즘이 high bias를 겪는다면, 더 많은 training data를 가지는 것이 별 도움이 되지 않는다.

Experiencing high variance
- Low training set size: Jtrain(θ)는 낮고 JCV(θ)는 높다.
- Large training set size: Jtrain(θ)는 training set size와 함께 증가하고 JCV(θ)는 레벨링 오프 없이 계속해서 감소한다. 또한 Jtrain(θ)<JCV(θ)이지만, 둘 간의 차이는 분명히 존재한다.
만약 학습 알고리즘이 high variance를 겪는다면 더 많은 training data를 가지는 것이 도움이 된다.
Deciding What to do Next Revisited
선택 프로세스는 다음과 같이 쪼개진다. 우선 high variance의 경우 이런 방법들을 추천한다.
- 더 많은 training example 가지기
- feature set를 줄이기
- λ를 증가시키기
반대로 high bias의 경우 이런 방법들을 추천한다.
- feature 추가하기
- polynomial feature 추가하기
- λ를 감소시키기
신경망 네트워크 진단
- 적은 파라미터를 사용하는 신경망 네트워크는 underfitting될 가능성이 있다. 하지만 계산 비용은 적다.
- 더 많은 파라미터를 사용하는 큰 신경망 네트워크는 overfitting될 가능성이 있다. 하지만 계산 비용은 크다. 이 경우에는 정규화를 사용(λ값 증가시키기)하여 overfitting을 해결할 수 있다.
하나의 hidden layer을 사용하는 것이 좋은 시작 기본값이다. cross validation set를 사용해서 여러 개의 hidden layer에서 신경망 네트워크를 학습시킬 수 있다. 그 중에 가장 좋은 성능을 보여주는 모델을 선택하면 된다.
모델 복잡도 효과
- lower-order polynomial(낮은 모델 복잡도)은 high bais와 low variance를 가진다. 이 경우에 모델은 일관적으로 좋지 않은 성능을 보여준다.
- higher-order polynomial(높은 모델 복잡도)은 training data에는 잘 적용되지만, test data에서는 좋지 않은 성능을 보여준다. 이는 training data에 대해 low bias를 가지고 high variance를 가지게 된다.
- 실제로, 잘 일반화할 수 있지만 데이터에 합리적으로 잘 맞는 중간 어딘가에 있는 모델을 선택해야 한다.
'Lecture 🧑🏫 > Coursera' 카테고리의 다른 글
| [Machine Learning] Machine Learning Algorithm Application (0) | 2023.03.28 |
|---|---|
| [Machine Learning] Evaluating a Learning Algorithm (0) | 2023.03.27 |
| [Machine Learning] Backpropagation in Practice (0) | 2023.03.27 |
| [Machine Learning] Cost Function & Backpropagation (0) | 2023.03.26 |
| [Machine Learning] Neural Networks (0) | 2023.03.20 |
