Gradient Checking
Gradient checkin 즉, 기울기 체크는 역전파가 의도한 대로 잘 되고 있는지 보장해준다. cost function의 미분을 다음을 사용하여 근사할 수 있다.
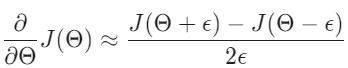
여러 개의 세타 행렬을 사용하면, $\theta_{j}$에 관한 미분을 다음과 같이 근사할 수 있다.

$\epsilon$은 $\epsilon = 10^{-4}$ 같은 작은 값이어야 적절하게 잘 작동한다는 것을 알 수 있다. $\epsilon$의 값이 너무 작으면 수치적 문제가 발생할 수도 있다. 그래서 $\theta_{j}$ 행렬에 epsilon을 추가하거나 빼기만 한다.
이전에 deltaVector를 어떻게 계산하는지에 대해 알아보았다. 그래서 gradApprox를 계산할 수 있게 되면, $gradApprox \approx deltaVector$라는 것을 확인할 수 있다.
역전파 알고리즘이 잘 작동되고 있다는 걸 확인하게 되면 gradApprox를 다시 계산할 필요는 없다. 왜냐하면 gradApprox를 계산하기 위한 코드는 매우 느리기 때문이다.. $($computationally expensive$)$
Random Initialization
모든 세타 가중치를 0으로 초기화하는 것은 신경망 네트워크에서 잘 작동하지 않는다. 역전파를 할 때, 모든 노드는 반복적으로 같은 값으로 업데이트되기 때문이다. 그 대신에 다음의 method를 사용하여 $\theta$ 행렬에 대한 가중치를 랜덤하게 초기화할 수 있다.

각각의 $\theta_{ij}^{(l)}$를 $[- \epsilon, \epsilon]$ 사이의 랜덤한 값으로 초기화한다. 위의 공식을 사용하는 것은 의도한 경계를 얻을 수 있도록 보장해준다. 똑같은 프로시저가 모든 $\theta$에 똑같이 적용된다.
Putting it Together
먼저 네트워크 architecture을 고른 뒤에, hidden layer의 유닛 수를 어떻게 할 지, 총 몇 개의 레이어를 가질 지 등을 포함하여 신경망 네트워크의 레이아웃을 선택한다.
- input unit의 수: feature $x^{(i)}$의 차원
- output unit의 수: 클래스의 수
- 각 레이어의 hidden unit의 수: 많으면 많을수록 좋긴 함. $($계산 비용과 밸런스를 맞춰서 선택하는 것이 중요$)$
- 기본갑: 1개의 hidden layer. 만약 1개 이상의 hidden layer를 가지면, 모든 hidden layer에서 똑같은 수의 unit을 가지기를 추천함.
Training a Neural Network
- 랜덤하게 가중치를 초기화
- 어떤 값 $x^{(i)}$에 대해 $h_{\theta}(x^{(i)})$를 얻기 위해 순전파를 수행
- cost function을 구현
- 역전파를 진행하여 편미분값을 계산
- gradient checking을 사용하여 역전파가 잘 작동하는지 확인. 그 다음에 gradient checking을 disable
- gradient descent 또는 다른 최적화 함수를 사용하여 cost function의 값을 최소화
순전파와 역전파를 진행할 때, 매 training example에서 루프를 한다. 다음의 그림은 신경망 네트워크에 위 방법들을 구현하였을 때 일어나는 모습들을 보여준다.

이상적으로 $h_{\theta}(x^{(i)}) \approx y^{(i)}$를 원한다. 위의 방법들은 cost function을 최소화하는데 도움을 준다. 하지만 $J(\theta)$는 완벽한 최댓값이 아니기 때문에 local minimum에 머물 수도 있다는 점을 기억하고 있도록 하자.
'Lecture 🧑🏫 > Coursera' 카테고리의 다른 글
| [Machine Learning] Bias vs Variance (0) | 2023.03.27 |
|---|---|
| [Machine Learning] Evaluating a Learning Algorithm (0) | 2023.03.27 |
| [Machine Learning] Cost Function & Backpropagation (0) | 2023.03.26 |
| [Machine Learning] Neural Networks (0) | 2023.03.20 |
| [Machine Learning] Solving the Problem of Overfitting (2) | 2023.03.20 |
