Cost Function
cost function을 설명할 때 사용할 몇 개의 변수들을 정의해보도록 하자.
- $L$: 네트워크에 있는 총 레이어의 수
- $s_l$: 레이어 $l$에 있는 unit의 수
- $K$: 출력 유닛과 클래스의 수
이 변수들을 신경망 네트워크에서 떠올려보면, 많은 출력 노드들을 가지게 될 것이다. $h_{\theta}(x)_{k}$는 $k$번째 출력으로 결과로 내놓는 hypothesis를 나타낸다. 신경망을 위한 cost function은 우리가 logistic function에서 사용한 것의 일반화이다. 정규화된 logistic regression의 cost function을 떠올려보도록 하자.
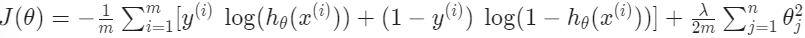
신경망 네트워크에 대해서는 이것의 형태가 살짝 바뀌게 된다.
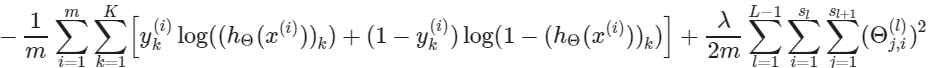
여러 개의 출력 노드를 설명하기 위해 몇 개의 시그마를 추가하였다. 대괄호 이전의 방정식 앞부분을 보면, 출력 노드의 수를 통하는 추가적인 시그마를 가지고 있다.
대괄호 이후 부분의 정규화 부분에서 여러 개의 세타 행렬을 설명할 필요가 있다. 현재 세타 행렬에 있는 열의 수는 현재 레이어에서 노드의 수와 같다고 볼 수 있다. 현재 세타 행렬에서 행의 수는 다음 레이어에서 노드의 수와 같다. logistic regression과 마찬가지로 모든 항들을 제곱하였다.
Backpropagation Algotirhm
'역전파'는 cost function을 최소화하는 신경망 네트워크의 용어이다. 이는 logistic & linear regression에서 하는 gradient secent와 유사하다. 역전파의 목표는 $min_{\theta}J(\theta)$를 계산하는 것이다. 세타에서 최적의 파라미터 세트를 사용해서 cost function $J$를 최소화하는 것이 목표인 셈이다. 이 섹션에서는 $J(\theta)$의 편미분을 계산하기 위해 사용할 방정식에 대해 알아볼 것이다: $\frac {\partial }{\partial \theta_{i,j}^{(l)}}J(\theta)$ 이를 위해 다음의 알고리즘을 사용한다.
Backpropagation Algorithm
학습 세트 ${(x^{(1)}, y^{(1)}) \cdots (x^{(m)}, y^{(m)})}$이 주어지면
- 모든 $(l, i, j)$에 대해 $\Delta_{i, j}^{(l)} := 0$으로 설정된다.
학습 예시 $t = 1$ to $m$에 대해
- $a^{(1)} := x^{(t)}$으로 설정된다.
- 순전파를 수행해서 $l = 2, 3, \cdots, L$에 대해 $a^{(l)}$을 계산한다.
- $y^{(t)}$를 사용해서 $\delta^{(L)} = a^{(L)} - y^{(t)}$을 계산한다. 여기서 $L$은 총 레이어의 수이고, $a^{(L)}$은 마지막 레이어에 대한 활성화 유닛의 출력 벡터이다. 그래서 마지막 레이어의 '오차값'은 마지막 레이어의 결괏값과 정확한 출력값 $y$ 간의 차이를 나타낸다.
- $\delta^{(l)} = ((\theta^{(l)})^{T} \delta^{(l+1)}. * a^{(l)}. * (1-a^{(l)}))$을 사용해서 $\delta^{(L-1)}, \delta^{(L-2), \cdots, \delta^{(2)}}$을 계산한다. 레이어 $l$의 델타값은 다음 레이어의 델타값과 레이어 $l$의 세타 행렬과 곱해져서 계산된다. 그 다음에 이 값을 $g^{'}$라고 불리는 함수와 element-wise 곱한다. 이 함수는 활성화 함수 $g$의 미분값이고 주어진 입력값 $z^{(l)}$에 의해 평가된다. $g^{'}$의 미분항은 다음과 같이 쓸 수 있다. $g^{'}(z^{(l)}) = a^{(l)}. * (1-a^{(l)})$
- $\Delta_{i, j}^{(l)} := \Delta_{i, j}^{(l)} + a_{j}^{(l)}\delta_{i}^{(l+1)}$ 또는 벡터화를 사용해서 $\Delta^{(l)} := \Delta^{(l)} + \delta^{(l+1)}(a^{(l)})^{T}$
그래서 다음과 같이 $\Delta$ 행렬을 업데이트한다.
- $D_{i, j}^{(l)} := \frac {1}{m}(\Delta_{i, j}^{(l)} + \lambda \theta_{i, j}^{(l)})$ 만약 $j \neq 0$이면
- $D_{i, j}^{(l)} := \frac {1}{m} \Delta_{i, j}^{(l)}$ 만약 $j = 0$이면
대문자 델타 행렬 $D$는 '누산기'로 사용되서 값을 더하고 결국 편미분을 계산한다. 따라서 다음 값을 얻게 된다: $\frac {\partial}{\partial \theta_{i, j}^{(l)}} J(\theta) = D_{i, j}^{(l)}$
Backpropagation Intuition
신경망 네트워크에 대한 cost function을 다시 떠올려보도록 하자.
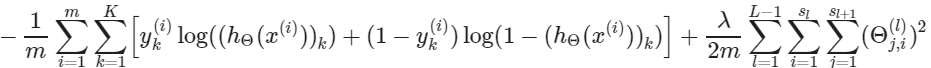
만약 간단한 비다중 클래스 분류 $(k=1)$과 정규화를 무시하면, cost는 다음과 같이 계산된다.
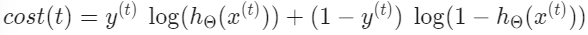
직관적으로 $\delta_{j}^{(l)}$은 $a_{j}^{(l)}$에 대한 '오차'값이다 $($unit j와 layer l$)$. 더욱 공식적으로 델타값은 사실상 cost function의 미분값이다.
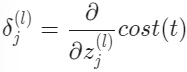
미분은 cost function에 접하는 선의 기울기이므로 기울기가 가파를수록 더 부정확하다. 아래의 신경망을 고려하고 $\delta_{j}^{(l)}$를 계산하는 방법을 살펴보겠다.
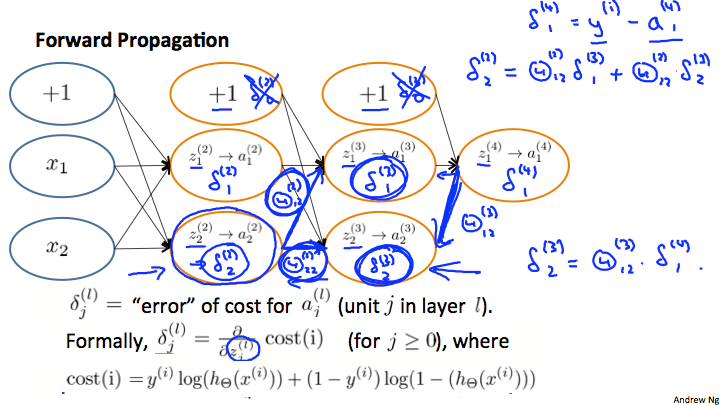
위의 이미지에서 $\delta_{2}^{(2)}$를 계산하기 위해 가중치 $\theta_{12}^{(2)}$와 $\theta_{22}^{(2)}$를 각각의 edge의 오른쪽 델타값과 곱하였다. 그래서 $\delta_{2}^{(2)} = \theta_{12}^{(2)} * \delta_{1}^{(3)} + \theta_{22}^{(2)} * \delta_{2}^{(3)}$을 얻을 수 있다. $\delta_{j}^{(l)}$의 모든 가능성을 계산하기 위해 다이어그램의 오른쪽에서부터 시작한다. edge를 $\theta_{ij}$로 생각할 수 있다. 오른쪽에서 부터 시작해서 왼쪽으로 가서 $\delta_{j}^{(l)}$의 값을 계산하기 위해, $\delta$와 각 가중치를 곱한 값의 모든 합을 구한다. 다른 예시를 생각해보면 $\delta_{2}^{(3)} = \theta_{12}^{(3)} * \delta_{1}^{(4)}$가 된다.
'Lecture 🧑🏫 > Coursera' 카테고리의 다른 글
| [Machine Learning] Evaluating a Learning Algorithm (0) | 2023.03.27 |
|---|---|
| [Machine Learning] Backpropagation in Practice (0) | 2023.03.27 |
| [Machine Learning] Neural Networks (0) | 2023.03.20 |
| [Machine Learning] Solving the Problem of Overfitting (2) | 2023.03.20 |
| [Machine Learning] Multiclass Classification (0) | 2023.03.15 |
