What is the purpose of this post?
이번 포스트에서는 CNN network의 역사에 대해 알아보았다. CNN에는 여러가지 network가 있었는데, 예를 들어 LeNet과 AlexNet 등이 있었다. 이번 포스트에서는 어떠한 CNN network들이 있었는지 알아보았다.
Table of Contents
1. LeNet
2. AlexNet
3. VGGNet
4. GoogLeNet
5. ResNet
6. ResNeXt
7. Xception
8. MobileNet
9. DenseNet
10. EfficientNet
11. ConvNext
1. LeNet$($1998$)$ Gradient-Based Learning Applied to Document Recognition
LeNet은 손글씨 숫자를 인식하는 네트워크로, 1998년에 제안되었다. 다음의 그림 1과 같이 합성곱 계층과 풀링 계층을 반복하고, 마지막으로 완전연결$($fully-connected$)$ 계층을 거치면서 결과를 출력한다.

LeNet과 '현재의 CNN'을 비교하면 몇 가지 면에서 차이가 난다.
- LeNet은 sigmoid 함수를 활용하는 반면, 현재의 CNN에서는 주로 ReLU를 사용한다.
- LeNet은 서브샘플링을 하면서 중간 데이터의 크기를 줄이지만, 현재는 최대 풀링을 주로 사용한다.
이처럼 LeNet과 현재의 CNN 사이에는 얼마간의 차이점이 존재한다.
2. AlexNet$($2012$)$ ImageNet Classification with Deep Convolutional Neural Networks
LeNet과 비교하여 훨씬 최근인 2012년에 발표된 AlexNet은 딥러닝 열풍을 일으키는데 큰 역할을 하였다. 그림 2에서 볼 수 있듯이 전체적인 구성을 기본적인 LeNet과 크게 다르지 않다.

AlexNet은 합성곱 계층과 풀링 계층을 거듭하며 마지막으로 완전연결 계층을 거쳐 결과를 출력한다. LeNet과 큰 구조는 바뀌지 않았지만, AlexNet에는 다음과 같은 변화가 주어졌다.
- 활성화 함수로 ReLU 함수를 사용함
- Local Response Normalization$($LRN$)$이라는 국소적 정규화를 실시하는 계층을 이용함
- dropout을 사용함
위의 내용들에서 알 수 있듯이 LeNet과 AlexNet의 전체적인 구조는 크게 바뀌지 않았다. 하지만, 이를 둘러싼 환경과 컴퓨터 기술이 진보를 이룬 것이다.
3. VGGNet$($2014$)$ Very Deep Convolutional Networks for Large-Scale Image Recognition
VGG는 합성곱 계층과 풀링 계층으로 구성된 기본적인 CNN이다. 다만, 그림 3과 같이 비중 있는 층$($합성곱 계층, 완전연결 계층$)$을 모두 16층으로 심화한 게 특징이다.

VGGNet에서 주목할 점은 $3 \times 3$의 작은 필터를 사용한 합성곱 계층을 연속으로 거친다는 것이다. 그림 2에서 알 수 있듯이 합성곱 계층을 2~4회 연속으로 풀링 계층을 두어 크기를 절반으로 줄이는 처리를 반복한다. 그리고 마지막에는 완전연결 계층을 통과시켜 결과를 출력한다.
VGGNet은 2014년 대회에서 GoogLeNet에 밀려 2위를 차지하기는 했지만, 구성이 간단하여 응용하기 좋다는 장점으로 많은 사랑을 받았었다.
4. GoogLeNet$($2014$)$ Going Deeper with Convolutions
GoogLeNet의 구성은 다음의 그림 4와 같다. 그림의 사각형이 합성곱 계층과 풀링 계층 등의 계층을 나타낸다.

그림을 보면 매우 복잡해 보이는데, 기본적으로는 지금까지 봐온 CNN과 다르지 않다. 단, GoogLeNet은 세로 방향 깊이뿐 아니라 가로 방향도 깊다는 것이 특징이다.
GoogLeNet에는 가로 방향에 '폭'이 있다. 이를 인셉션 구조라고 하며, 그 기반 구조는 그림 5와 같다.

인셉션 구조는 그림 5와 같이 크기가 다른 필터와 풀링을 여러 개 적용하여 그 결과를 결합한다. 이 인셉션 구조를 하나의 빌딩 블록으로 사용하는 것이 GoogLeNet의 특징인 것이다. 또한 GoogLeNet에서는 $1 \times 1$ 크기의 필터를 사용한 합성곱 계층을 많은 곳에서 사용한다. 이 $1 \times 1$의 합성곱 연산은 채널 쪽으로 크기를 줄이는 것으로, 매개변수 제거와 고속 처리에 기여한다.
일반적으로 생각해보면, 모델의 깊이가 깊어졌을 때, 성능은 상승할 것이라고 생각될 것이다. 하지만, 실제로는 그렇지 않다. 왜냐하면 bigger 모델은 shallow 모델보다 더욱 오버피팅이 되있기 때문일 것이다. 실제로 56개의 레이어를 갖는 모델보다 20개의 레이어를 갖는 모델이 더 나은 성능을 보여준다. 그렇다면 모델의 깊이가 길어질수록 어떤 일이 발생하는 걸까? 그것은 바로 Vanishing Gradient Problem이다. 실제로, sigmoid 함수의 기울기는 0.25보다 작고, chain rule이 적용된다면 전반적인 기울기의 값은 더욱 작아질 것이다. 그렇다면 어떻게 해야 더욱 깊은 모델이 얕은 모델보다 최소한 더 나은 성능을 보여줄 수가 있을까? 이에 대한 대답을 ResNet에서 하였다.
5. ResNet$($2015$)$ Deep Residual Learning for Image Recognition
ResNet은 마이크로소프트 팀이 개발한 네트워크이다. 그 특징은 지금까지보다 층을 더욱 깊게 할 수 있는 특별한 '장치'에 있다.
지금까지는 층을 깊게 하는 것이 성능 향상에 중요하다고 알려져 있었다. 그러나 딥러닝의 학습에서는 층이 지나치게 깊으면 학습이 잘 되지 않고, 오히려 성능이 떨어지는 경우도 많다. ResNet에서는 그런 문제를 해결하기 위해 스킵 연결$($skip connection$)$을 도입하였다. 이 구조가 층의 깊이에 비례해 성능을 향상시킬 수 있게 한 핵심이다. 스킵 연결이란 그림 6과 같이 입력 데이터를 합성곱 계층을 건너뛰어 출력에 바로 더해주는 구조를 말한다.

그림 6에서는 입력 $x$를 연속한 두 합성곱 계층을 건너뛰어 출력에 바로 연결한다. 이 단축 경로가 없었다면 두 합성곱 계층의 출력이 $F(x)$가 되나, 스킵 연결로 인해 $F(x) + x$가 되는 것이 핵심이다. 스킵 연결은 층이 깊어져도 학습을 효율적으로 할 수 있도록 해주는데, 이는 역전파 때 스킵 연결이 신호 감쇠를 막아주기 때문이다. ResNet에서는 $F(x) - x$가 0에 수렴하도록 학습시켜야 한다. 한 마디로, 어떤 $x$가 들어온다고 해도 residual이 0을 갖도록 갖도록 학습시키는 것이 더욱 좋은 학습 효과를 불러올 것에서 시작된 발상이다.
스킵 연결을 입력 데이터를 '그대로' 흘려주는 것으로, 역전파 때도 상류의 기울기를 그대로 하류로 보낸다. 여기에서의 핵심은 상류의 기울기에 아무런 수정도 가하지 않고, '그대로' 흘려보내준다는 것이다. 그래서 스킵 연결로 기울기가 작아지거나 지나치게 커질 걱정 없이 앞 층에 '의미 있는 기울기'가 전해지리라 기대할 수 있다. 층을 깊게 할수록 기울기가 작아지는 소실 문제를 이 스킵 연결이 줄여주는 것이다.
ResNet은 앞서 설명한 VGGNet을 기반으로 스킵 연결을 도입하여 층을 깊게 하였다. 그 결과 다음의 그림 7과 같은 결과가 나왔다.

그림 7과 같이 ResNet은 합성곱 계층을 2개 층마다 건너뛰면서 층을 깊게 한다. 실험 결과 150층 이상으로 해도 정확도가 오르는 모습을 확인할 수 있다.
6. ResNeXt$($2017$)$ Aggregated Residual Transformations for Deep Neural Networks
ResNeXt는 ResNet의 bottleneck을 아래 그림과 같이 수정한 모델이다.

기존의 ResNet에서는 256차원의 입력이 들어오면, 256개의 채널의 입력값이 Bottleneck으로 전달되고 $1 \times 1$의 conv를 지나서 64개의 채널을 가진다. 그러고 여기서 64개의 채널을 $3 \times 3$의 conv를 지나서 다시 64개의 채널을 가진 뒤, 마지막으로 64개의 채널은 $1 \times 1$ conv를 지나서 다시 256의 채널을 갖는 출력을 내놓는다.
하지만 여기서 ResNeXt는 256개의 채널의 입력값이 Bottleneck으로 전달되고, $1 \times 1$의 conv를 거쳐서 128개의 채널을 가진다. 여기서 128개의 채널을 32개의 그룹으로 분할하여 각 그룹당 $($128/32$)$의 채널이 된다. 그리고 32개의 conv는 4개의 채널 입력값애 대해서만 연산을 수행해 4채널의 피쳐맵을 생성한다. 32개의 그룹에서 생성한 4개의 피쳐맵을 연결하여 128개의 채널을 만든다. 다음에 $1 \times 1$ conv를 거쳐서 256개의 채널이 된다. 그리고 이 32는 cardinality라는 하이퍼파라미터로 조절 가능한 변수이다.
논문의 저자는 cardinality를 증가시키는 것이 width나 depth를 증가시키는 것보다 효과적이라는 것을 보여줬다.
7. Xception$($2017$)$
Xception은 Inception을 개선시킨 모델로, 기존의 Inception에서 사용되는 convolutional layer을 modified depthwise separable convolution으로 대체시키고, residual connection을 추가적으로 사용한 모델이다.
original depthwise convolution의 구조는 다음과 같다.

original depthwise separable convolution은 입력 데이터에 대해 depthwise convolution을 수행하고, 그 결과에 pointwise convolution을 수행한다. 이 둘을 살펴보면 다음과 같다.
- Depthwise convolution은 입력 채널 각각에 독립적으로 $n \times n$의 conv를 수행한다. 입력 채널에 대해 conv를 수행하고, 각각 입력값과 동일한 크기의 피쳐맵을 생성한다.
- Pointwise convolution은 $1 \times 1$ 크기의 conv로, 차원의 크기를 변경시키고, 채널의 수를 조절한다.
기존의 합성곱과 비교하면, 모든 채널에 대해 합성곱을 진행할 필요가 없다. 이것은 connection의 수가 적고, 모델은 더욱 가볍다라는 의미이다.
논문에서는 이러한 Depthwise Separable Convolution을 modify하여 Xception에 사용하였는데, 이것이 바로 Modified Depthwise Separable Convolution이다.

이 Modified Depthwise Separable Convolution은 기존의 방법과 반대로, pointwise convolution이 먼저 수행되고, 그 결과에 depthwise convolution이 수행된다. 이러한 수정은 Inception V3에서 처음에 $n \times n$ sparial convolution에 $1 \times 1$ convolution을 수행하는 것으로부터 따왔다.
기존의 Inception과 depthwise convolution 사이에는 두 가지 정도 차이점이 존재한다.
- operation 순서: depthwise separable convolution은 channel-wise spatial convolution이 먼저 수행되지만, Inception은 $1 \times 1$ convolution이 먼저 수행된다.
- 비선형의 유무: Inception은 모든 operation이 ReLU에 의해 비선형성을 지니지만, depthwise separable convolution은 비선형성을 지니지 않는다. 깊이가 깊은 모델에 대해서 비선형성을 가진다는 것은 더욱 잘 학습되도록 도와주지만, 깊이가 얕은 모델에 대해서는 비선형성이 오히려 모델의 성능을 해치는 요소가 된다. 그래서 Xception은 모든 활성화함수를 없앴을 때, 가장 좋은 성능을 보여줬다.
Xception의 전반적인 architecture는 다음의 그림 11과 같다.

위의 그림에서 'SeparableConv'는 Modified Depthwise Separable Convolution을 의미한다. 그리고 위 그림에서 알 수 있듯이 residual connection이 추가적으로 사용된다. 이 residual network의 유무에 따라 모델의 성능이 엄청나게 변화한다.
8. MobileNet$($2017$)$ Efficient Convolutional Neural Networks for Mobile Vision Applications
MobileNet은 Xception과 마찬가지로 depthwise separable convolution에 기반을 둔 방법이다. 하지만, MobileNet은 모바일 기기에서도 사용할 수 있을만큼 가벼운 크기의 모델을 만드는 데에 중점을 두었다. 그래서 이를 위해 MobileNet에서는 두 개의 새로운 parameter을 소개한다.
기존의 convolutional layer는 filtering과 combining을 하나의 스텝에서 진행하는데, depthwise separable convolution은 이 과정을 두 개의 layer로 분할하였다. 이러한 분할은 계산량과 모델의 크기를 엄청나게 줄이는 데 도움이 되었다. 다음의 그림 12는 기존의 convolution$($a$)$이 어떻게 depthwise convolution$($b$)$와 $1 \times 1$의 pointwise convolution으로 분할되었는지 보여주고 있다.

기존의 convolutional layer는 입력으로 $D_{F} \times D_{F} \times M$의 피쳐맵 $\textbf{F}$를 가지고, $D_{F} \times D_{F} \times N$의 피쳐맵 $\textbf{G}$를 가진다. 여기서 $D_{F}$는 square 입력 피쳐맵의 공간적 width와 height이다. $M$은 입력 채널의 수이고, $D_{G}$는 square 출력 피쳐맵의 공간적 width와 height이다. 마지막으로 $N$은 출력 채널의 수이다.
기존의 convolutional layer은 크기 $D_{K} \times D_{K} \times M \times N$의 커널 $\textbf{K}$에 의해 파라미터화 된다. 야기서 $D_{K}$는 커널의 공간적 차원이고, $M$은 입력 채널의 수이고, $N$은 출력 채널의 수이다. 기존의 convolution에 대한 출력 피쳐맵은 다음과 같이 계산된다.

따라서 기존 convolution의 계산 비용은 다음과 같다.

depthwise separable convolution은 계산 비용을 줄이기 위해 기존의 convolution의 filtering과 combining을 따로 분리하였다. 각 입력 채널에 한 개의 필터를 씌운 depthwise convolution은 다음과 같이 쓰일 수 있다.

여기서 $\hat{\textbf{K}}$는 크기가 $D_{K} \times D_{K} \times M$인 depthwise convolutional 커널이다. 여기서 $\hat{\textbf{K}}$의 $m$번째 필터는 $\textbf{F}$의 $m$번째 채널에 적용되서 필터링된 출력 피쳐맵 $\hat{\textbf{G}}$의 $m$번째 채널을 생성한다. 이때 depthwise convolution의 계산 비용은 다음과 같다.

여기서 $1 \times 1$의 pointwise convolution이 추가된 depthwise separable convolution의 계산 비용은 다음과 같다. 앞의 항이 depthwise의 계산 비용이고, 뒤의 항이 pointwise의 계산 비용이다.

Width Multiplier: Thinner Models
모델을 더욱 작고 빠르게 만들기 위해서 width multiplier라고 불리는 파라미터 $\alpha$를 소개하였다. 이 width multiplier $\alpha$의 역할은 각 레이어에서 네트워크를 균일하게 얇게 만들어 준다. widthe multiplier $\alpha$와 레이어가 주어지면, 입력 채널 $M$은 $\alpha M$이 되고, 출력 채널 $N$은 $\alpha N$이 된다. width multiplier $\alpha$와 함께 하는 depthwise separable convolution의 계산 비용은 다음과 같아진다.

여기서 $\alpha \in (0,1]$이고, $\alpha = 1$이 MobileNet의 baseline이고, $\alpha < 1$이면, 축소된 MobileNet이다.
Resolution Multiplier: Reduced Representation
모델의 계산 비용을 줄이기 위한 두 번째 하이퍼 파라미터는 resolution multiplier $\rho $이다. 이것을 입력 이미지와 각 레이어의 중간 representation에 적용한 이유는 부수적으로 계산 비용을 줄이기 위해서이다. width multiplier $\alpha$와 resolution multiplier $\rho$를 이용하여 depthwise separable convolution의 계산 비용을 나타내면 다음과 같다.

여기서 $\rho \in (0,1]$이고, $\rho = 1$이면 baseline이고, $\rho < 1$이면 축소된 MobileNet이다.
9. DenseNet$($2017$)$ Densely Connected Convolutional Networks
DenseNet은 기존의 convolutional network에서 사용되는 connection의 수를 늘리고, 이전 layer들의 모든 피쳐맵을 다음 layer의 입력으로 사용함으로써 다음과 같은 contribution을 보여줬다.
- vanishing gradient 문제 완화
- 더욱 강력한 feature propagation
- Feature reuse
- 감소된 parameter 수
Dense connections
network의 feed-forward 환경에서, dense 블록의 각 레이어는 모든 이전 레이어의 피쳐맵을 받고, 이전 레이어의 출력을 모든 subsequent 레이어에 전달한다. 이전 레이어들로부터 받아진 피쳐맵은 concatenation을 통해 합쳐진다. $($ResNet의 summation이 아니라$)$ 이러한 connection은 더 나은 gradient-flow를 허락해준다. 아래 그림 13은 Dense connection의 과정을 보여준다.

이러한 dense connection 때문에, 모델은 더 적은 레이어를 요구한다. 왜냐하면, 수집된 지식이 재사용되기 때문에, 불필요한 피쳐맵을 추가로 학습할 필요가 없기 때문이다. 제안된 architecture는 narrow layer을 가지고 있는데, 이는 12개의 채널의 피쳐맵 만으로도 SoTA를 달성할 수 있게 해줬다. 적고 비좁은 레이어는 모델이 적은 파라미터로도 학습될 수 있다는 것을 의미한다. 논문의 저자도 입력의 variation의 중요성을 얘기했는데, 이는 모델이 훈련 데이터로부터 오버피팅되는 것을 방지한다. 다음의 그림 14는 DenseNet의 architecture을 보여준다.

Composite function
각각의 network representation에서의 conv 블록은 BatchNorm -> ReLU -> $3 \times 3$ Conv의 모양을 가지고 있다.
Dense layer
각각의 dense-layer은 2개의 convolutional operation으로 구성되어 있다.
- $1 \times 1$ CONV: feature을 뽑아내기 위한 기본적인 conv operation
- $3 \times 3$ CONV: feature depth와 channel 수를 감소시킴
다음의 그림 15는 Dense Layer의 과정을 보여준다. 64개의 채널을 가진 입력이 들어오고, $1 \times 1$ conv layer을 지났을 때, channel의 수는 128이 된다. 그리고 여기에 다시 $3 \times 3$ conv layer을 지나게 되면 32개의 채널을 가진 출력이 나오게 된다.

Growth rage$($k$)$
이것은 논문에서 소개한 새로운 용어이다. 이것은 dense layer로부터 출력되는 채널의 수를 말한다. 저자들은 $k=32$인 값을 사용하였다. 이 말인 즉슨, dense layer $(l)$가 이전 dense layer $(l-1)$로부터 이 k 값만큼의 feature을 받는다는 의미이다. 이것이 growth rate로 불리기 되는데, 왜냐하면, 각각의 레이어는 32개의 채널 feature가 concatenate되고, 다음 레이어의 입력으로 들어가기 때문이다.

Transition layer
각 dense block의 마지막에서는, 피쳐맵의 수가 input features + $($number of dense layers $\times$ growth rate$)$으로 축적된다. 따라서, 64개의 채널 feature가 growth rate가 32인 6개의 dense layer의 dense block에 들어오면, 마지막 블록에서의 cosjf tnsms $64 + (6 \times 32) = 256$이 된다. 이 채널 수를 줄이려면, transition layer는 두 개의 dense block 사이에 추가되어야 한다. 그래서 transitoon layer는 다음과 같이 구성된다.

- $1 \times 1$ Conv operation: 채널의 수를 절반으로 줄여줌
- $2 \times 2$ AVG Pool operation: width와 height 면에서 feature를 downsampling 함
10. EfficientNet$($2019$)$ Rethinking Model Scaling for Convolutional Neural Networks
EfficientNet은 다음의 아이디어로부터 시작된다.
- 모델의 scaling 방법에 대한 학습
- network의 depth, width, resolution을 조심스럽게 balancing 해서 scaling을 하면 성능이 향상하지 않을까?
그래서 논문에서는 모든 차원의 depth/width/resolution을 간단하지만 효과적인 compound coefficient를 활용하여 균일하게 scaling 하는 새로운 scaling method을 제안하였다. 더 나아가서, 새로운 baseline network를 디자인하기 위해 신경망 architecture 검색을 사용하고, 이것을 scale up하여 family model 정도의 성능을 얻는 EfficientNet을 제안하였다.
지금까지의 scaling up method들은 width, depth, resolution 중 하나의 dimension만 scaling 하였다. 하지만, 만약 1개가 아니라, 그 이상의 2개 혹은 3개의 차원을 늘리는 것이 가능하다면 더욱 좋은 성능을 내지 않을까? 이러한 아이디어를 사용해보기 위해 논문에서는 width/depth/resolution 각각을 일정한 비율로 scaling 하면서 이들의 balance를 맞추었다. 다음의 그림 18은 기존의 baseline ConvNet의 scaling과 각각 width/depth/resolution scaling, 그리고 마지막으로 이것을 모두 합친 compound scaling을 보여주고 있다.

Compound Model Scaling
논문에서는 새로운 scaling method를 제안하였다. 기존의 ConvNet 같은 경우에는 다음과 같이 레이어를 거치면서 작동한다.

여기서 $\boldsymbol{F}^{L_{i}}_{i}$는 operator $\boldsymbol{F}_{i}$의 stage $i$에서 $L_{i}$만큼 반복하는 것이고, $\left< H_{i},W_{i},C_{i}\right>$는 레이어 $i$의 입력 텐서 $X$를 의미한다. 기존의 ConvNet에서는 spatial dimension이 시간이 지남에 따라 점차 감소한다. 따라서 width와 depth의 차원은 감소하는 반면, resolution의 차원은 상승한다. 예를 들어, $\left< 224,224,3\right>$의 입력이 들어가면, 출력으로 $\left< 7,7,512\right>$이 나오는 것이다.
기존의 ConvNet은 최적의 layer architecture $\boldsymbol{F}_{i}$를 찾는 것이 목표지만, model scaling은 기존의 baseline에서 $\boldsymbol{F}_{i}$를 건들지 않고, network의 length와 width, resolution을 확장시키는 것이다. model scaling의 목표를 수식으로 나타내면 다음과 같다. memory와 FLOPS는 최대한 덜 사용하고, accuracy는 최대화하는 것이 목표이다.

여기서 $d,w,r$은 scaling network를 위한 coefficient이고, $\hat{\boldsymbol{F}_{i}},\hat{\boldsymbol{L}_{i}},\hat{H_{i}},\hat{W_{i}},\hat{C_{i}}$는 사전에 정의도니 baseline network의 파라미터이다.
Scaling Dimensions
최적의 $d,w,r$을 찾는데 어려움이 있는 이유는, 각각이 서로에게 의존하고, 서로 다른 자원의 제약에서 값이 바뀌기 때문이다. 다음은 각 차원들에 대해서 scaling을 한 결과를 설명하고 있다.
- Depth $(d)$: network의 depth을 scaling 하는 것은 가장 일반적인 방법이다. 이를 통해, network는 더욱 길고 복잡한 feature을 파악할 수 있고, 새로운 task에 대해서 정규화를 잘한다는 장점이 있다. 하지만, 더욱 깊어진 모델은 vanishing gradient 문제 때문에 학습을 하기 어렵다는 문제점이 있다. 여러 방법들을 통해 이 vanishing gradient를 완하시키기는 했지만, 성능 향상이 사라진다는 단점이 있다. 다음의 그림 19의 가운데를 보면 서로 다른 depth coefficient $d$에 대해서 scaling을 진행했을 때, 성능을 보여주고 있다.
- Width $(w)$: network의 width를 scaling하는 것은 주로 small size model에서 이루어진다. 이를 통해, 더욱 세분화된 feature를 얻을 수 있고, training이 쉬워진다는 장점이 있다. 하지만, 매우 wide 하지만, shallow한 모델은 더욱 높은 수준의 feature을 얻기 어렵다는 단점이 있다. 그림 19의 왼쪽을 보면 더욱 큰 $w$에 대해 network가 wide해짐에 따라 accuracy가 더욱 빠르게 감소한다는 것을 알 수 있다.
- Resolution $(r)$: 더욱 높은 resolution은 더욱 세분화된 패턴을 파악할 수 있게 해준다. 그림 19의 오른쪽을 보면 실제로도 높은 resolution이 더 좋은 성능을 보여준다는 것을 알 수 있다.
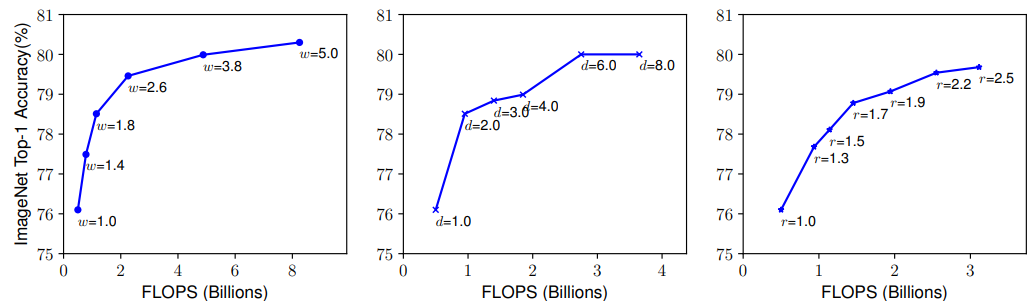
이를 통해 파악할 수 있었던 건, 확실히 scaling up이 성능 향상을 가져오긴 한다는 점이다. 다만, 이것은 bigger model에 대해서는 그렇게 큰 gain을 가져오지는 못 한다.
Compound Scaling
resolution의 차원이 상승하게 되면, width의 차원 또한 상승하게 된다. 왜냐하면, 더욱 세분화된 feature을 가져오기 위해서이다. 이것을 검증하기 위해서, 서로 다른 depth와 resolution 아래에서 width scaling을 진행하였다. depth와 resolution의 변화 없이, 오직 network width $w$만을 scale하면 accuracy는 빠르게 수렴한다. 그리고 더욱 깊은 depth와 resolution에 대해서는 똑같은 FLOPS 아래에서 더욱 좋은 성능을 보여준다. 이의 결과를 다음의 그림 20에서 확인할 수 있다.

이를 통해 파악할 수 있었던 점은 모든 차원 간의 balance가 성능 향상에 매우 중요하다는 것이다.
논문에서는 새로운 compound scaling method를 제안한다. 여기에서는 network의 depth, width, resolution을 균일하게 scale하기 위해 compound coefficient $\phi $를 사용한다.

여기서 $\alpha,\beta,\gamma$는 small grid search에 의해 결정되는 정수이다. 직관적으로 φ는 모델 스케일링에 사용할 수 있는 추가 리소스를 제어하는 사용자 지정 계수이며, α, β, γ는 이러한 추가 리소스를 각각 network의 width, septh 및 resolution에 할당하는 방법을 지정한다.
EfficientNet Architecture
논문에서는 accuracy와 FLOPS 모두를 optimize하는 multi-objective 신경망 architecture search를 leveraging 함으로써 baseline architecture을 제작하였다. 이전의 연구와 똑같은 research space를 사용하였고, $ACC(m) \times [FLOPS(m)/T]^{w}$를 optimization의 골로 사용하였다. 여기서 $ACC(m)$과 $FLOPS(m)$은 모델 $m$의 accuracy와 FLOPS를 나타내고, $T$는 target-FLOPS, $w=-0.07$은 accuracy와 FLOPS 간의 trade-off를 컨트롤하는 하이퍼파라미터이다.
baseline EfficientNet-B0을 살펴보면, compound scaling method를 다음의 구 자리 단계로 적용하여 scale up을 진행하였다.
- STEP 1: 먼저 가용 자원이 두 배 더 많다고 가정하고 $\phi=1$로 고정하였고, 수식 2와 3을 기반으로 $\alpha, \beta, \gamma$의 작은 그리드 검색을 수행한다. 특히, 제약 조건 $\alpha\cdot \beta^{2} \cdot \gamma^{2}\approx 2$ 아래에서, EfficientNet-B0의 최적의 값은 $\alpha=1.2,\beta=1.1,\gamma=1.15$였다.
- STEP 2: EfficientNet-B1부터 B7을 얻기 위해, $\alpha,\beta,\gamma$를 정수로 고정하고, 서로 다른 $\phi$를 사용하면서 baseline network를 scale up 하였다.
논문에서는 첫 번째, small baseline network에서 search를 진행하고, 두 번째, 모든 서로 다른 모델에 대해 똑같은 scaling coefficient를 사용하였다.
11. ConvNeXt$($2022$)$ A ConvNet for the 2020s
Vision Transformer는 computer vision 분야에서도 Transformer 모델이 좋은 성능을 보여줄 수 있다는 것을 보여주었다. 하지만, 일반적인 computer vision task들에 대해서는 어려움을 느끼는 모습을 보여줬다. 이를 해결하기 위해, 계급형 Transformer인 Swin Tansformer을 소개하였다. 하지만, 이러한 방법들은 어떠한 특별한 bias를 이용한 것이 아니라 그저 Transformer의 우월함을 이용한 기법에 불과하였다. 따라서, 논문에서는 design space를 다시 검사하고, 순수 ConvNet이 달성할 수 있는 것의 한계를 테스트하였다. 그러기 위해 기본적인 ResNet을 vision Transformer의 디자인처럼 modernize 하였다.
Modernizing a ConvNet: a Roadmap
논문에서는 ResNet에서 Transformer와 유사한 ConvNet으로 가는 궤적을 공개하였다. 논문에서는 original ResNet-50 model에 대해서 훈련을 진행하고, 이것을 baseline model로 삼았다. 그리고 디자인 선택은 다음과 같이 요약할 수 있다. 1$)$ macro design, 2$)$ ResNeXt, 3$)$ inverted bottleneck, 4$)$ large kernel size, 5$)$ 다양한 layer-wise micro design으로 요약할 수 있다.
Training Techniques
training procedure도 모델의 성능에 영향을 준다. 예를 들어 vision Transformer도 새로운 module set와 architectural design을 가져올 뿐만 아니라, 새로운 training technique을 소개한다. 그래서, 논문에서는 baseline model에 대해 vision Transformer의 training technique을 적용하여 모델의 성능을 향상시켰다. 이를 통해 epochs의 수는 90에서 300으로 늘어났고, AdamW optimizer을 사용하였고, data augmentation 기술과 regularization scheme을 사용하였다.
Macro Design
논문에서는 Swin Transformer의 macro network를 분석하였다. Swin Transformer는 ConvNet을 따라서 각 stage가 서로 다른 feature map resolution을 가지는 곳에서 multi-stage design을 사용하였다. 여기에는 두 개의 흥미로운 design이 있는데, stage compute ratio와 "stem cell" 구조이다.
- Changing stage compute ratio: ResNet의 여러 단계에 걸친 계산 분포의 원래 설계는 대체로 경험적이었다. 무거운 "res4" stage는 detector head가 14×14 feature plane에서 작동하는 object detection과 같은 downstream task와 호환되도록 의도되었다. 반대로, Swin Transformer는 똑같은 원리를 따르지만, 살짝은 다른 stage compute ration인 $1:1:3:1$을 사용한다. 더욱 큰 Swin Transformer에 대해서, 비율은 $1:1:9:1$이 된다. 이 비율을 따라 ResNet-50의 stage를 $(3,4,6,3)$을 $(3,3,9,3)$으로 변경하였다. 이것은 또한 Swin Transformer와 함꼐 FLOPs를 정렬하였다. 논문에서는 stage compute ratio를 사용하였다.
- Changing stem to "Patchify": stem cell은 보통 network의 시작에서 어떻게 input image를 처리할 지와 같은 걱정이 있다. 그래서 stem cell은 적절한 크기의 입력을 만들기 위해 input image를 downsampling 한다. 기존의 ResNet은 stride가 2인 $7 \times 7$의 convolution을 진행하고, max pool을 진행한다. 그 결과, 입력 이미지를 4배 가량 downsampling 할 수 있다. vision Transformer에서는 더욱 큰 사이즈의 커널을 가지고 non-overlapping convolution인 새로운 "patchify" 전략을 stem cell로 사용한다. Swin Transformer는 비슷한 "patchify" 레이어를 사용하지만, 더욱 작은 크기의 patch size인 4를 사용한다. 그래서 논문에서는 ResNet-style의 stem cell을 stride가 4이고, 크기가 $4 \times 4$인 patchify 알고리즘을 사용한다.
ResNeXt-ify
이 파트에서는 ResNet보다 더 효율이 좋은 FLOPs로 더 좋은 성능을 뽑아내는 ResNeXt를 적용시키기 위해 시도하였다. 중요 요소는 grouped convolution인데, convolutional filter는 서로 다른 그룹으로 분리된다. ResNeXt의 원리는 "더 많은 그룹을 사용해서 폭을 넓혀라" 이다. 더 정확하게는, ResNeXt는 bottleneck block에서 $3 \times 3$ conv layer에 대해서 drouped convolution을 사용한다. 이것은 FLOPs를 확실히 줄여주고, network의 폭은 capacity loss를 보상하기 위해 확장된다.
논문에서는 depthwise convolution을 사용한다. depthwise convolution은 self-attention에서의 weighted sum과 비슷하다. depthwise의 사용은 network의 FLOPs를 줄였다. ResNeXt에서 제안된 전략을 따라서, 논문에서는 network의 폭을 Swin Transformer와 똑같은 채널 수로 증가시켰다 $($64 to 96$)$. 논문에서는 ResNeXt design을 사용하였다.
Inverted Bottleneck
모든 Transformer block에 대한 한 가지 중요한 design은 inverted bottleneck을 생성한다는 것이다. 흥미롭게도, 이러한 Transformer design은 ConvNet에서 사용되는 expansion 비율 4와 함께 inverted bottleneck에 연결된다.
다음 그림 21의 $($a$)$와 $($b$)$는 inverted bottleneck의 구조를 설명한다. depthwise convolution layer에 대해 증가된 FLOPs에도 불구하고, 이러한 변화는 downsampling residual block의 shortcut $1 \times 1$ conv layer에서 상당한 FLOPs 감소 때문에, 전체 network의 FLOPs를 줄게 만들었다. 논문에서는 inverted bottleneck을 사용하였다.

Large Kernel Sizes
- Moving up depthwise conv layer: 큰 커널을 알아보기 위해서는, depthwise conv layer의 position을 위로 올려야 한다는 하나의 필요 조건이 있다. $($그림 21의 b와 c$)$ 이것은 Transformer에서도 적용되는데, MAS block은 MLP 레이어보다 전에 있어야 한다. inverted bottleneck을 가지는 것처럼, 이것은 자연적인 design 선택이다. 복잡하고 비효과적인 모듈$($MSA, large-kernel conv$)$은 적은 채널의 수를 가질 것이고, 반면에 효과적인 dense $1 \times 1$ layer는 무거운 lifting을 할 것이다. 이 중간 과정은 FLOPs를 줄여주고, 일시적인 성능 저하를 주었다.
- Increasing the kernel size: 더욱 큰 kernel의 convolution을 적용시켰을 때의 장점은 상당한데, 논문에서는 다양한 크기의 kernel에 대해서 실험을 진행하였다. 예를 들어, 3, 5, 7, 9, 11의 크기에 대해서 말이다. 그 결과, $(7 \times 7)$ 크기의 kernel 부터는 성능이 수렴한다는 것을 알 수 있었다. 논문에서는 $(7 \times 7)$의 depthwise conv를 사용하였다.
Micro design
이 섹션에서는 activation function과 normalization layer에 대한 세부적인 선택에 초점을 두었다.
- Replacing ReLU with GELU: NLP와 computer vision의 차이점 중 하나는 어떠한 activation function을 활용하냐는 것이다. 수많은 activation function이 개발되었는데, 아직도 ConvNet에서는 ReLU를 사용한다. ReLU는 또한 original Transformer에서도 사용된다. GELU는 ReLU를 좀 더 다듬은 activation function으로 논문에서는 GELU를 사용하였다.
- Fewer activation functions: ResNet과 달리 Transformer는 좀 더 적은 수의 activation function을 가진다. 왜냐하면 ResNet은 모든 레이어에 대해서 activation function을 적용하는데, Transformer는 MLP block에서 오직 하나의 activation function을 사용하기 때문이다. 그래서 그림 22와 같이 두 개의 $1 \times 1$ 레이어 사이에 있는 하나를 제외하고, residual block에서 모든 GELU를 제거하였다. 논문에서는 하나의 GELU activation을 사용하였다.

- Fewer normalization layers: Transformer block은 보통 적은 normalization layer을 가진다. 그래서 두 개의 Batch Normalization을 지우고, 하나의 Batch Normalization만을 $1 \times 1$ conv layer 이전에 남겨 두었다.
- Substituting BN with LN: Batch Normalization은 수렴을 개선시키고, overfitting을 감소시켰다. 하지만, Batch Normalization은 많은 복잡성을 가지고 있어서, 모델의 성능에 해를 끼칠 수 있다. 그럼에도 불구하고, Batch Normalization은 많은 vision task에서 선호되는 normalization이다. 반면에, 간단한 Layer Normalization은 Transformer에서 사용되었고, 전반적인 task에 대해 좋은 성능을 보여줬다. 그래서 논문에서는 각 residual block에서 하나의 Layer Normalization을 사용하였다.
- Separate downsampling layers: ResNet에서 각 stage의 시작에서 residual block에 대해서 stride가 2인 $3 \times 3$ conv layer을 사용하여 spatial downsampling을 하였다. Swin Transformer에서는 stage 사이에 separate downsampling이 적용되었다. 논문에서는 downstream sampling을 위해 stride가 2인 $2 \times 2$ conv layer을 사용하였다.
- Closing remarks: 마침내 모든 걸 끝마치고, Swin Transformer을 능가하는 ConvNeXt를 개발하였다. 언급된 모든 design choice는 vision Transformer에서 적용된 것들이다. 추가적으로, 이러한 design들은 ConvNet 환경에서 새로운 기술들이 아니다. 이들은 개별적으로 연구된 기술들로, 종합적으로 연구되지 않았을 뿐이다. 논문의 ConvNeXt 모델은 Swin Transformer와 비교하여 FLOPs와 parameters, throughput, memory거의 동일하게 사용되었다. 하지만, 이동하는 window attention이나 relative position biases 같은 특별한 모듈을 요구하지 않는다.
참고문헌
Convolutional Neural Networks: A Brief History of their Evolution
In the world of deep learning, Convolutional Neural Network (CNN) is a class of artificial neural network, most commonly used for image…
medium.com
밑바닥부터 시작하는 딥러닝
https://arxiv.org/abs/1611.05431
https://arxiv.org/abs/1512.03385
https://arxiv.org/abs/1610.02357
Review: Xception — With Depthwise Separable Convolution, Better Than Inception-v3 (Image…
In this story, Xception [1] by Google, stands for Extreme version of Inception, is reviewed. With a modified depthwise separable…
towardsdatascience.com
https://arxiv.org/abs/1704.04861
https://arxiv.org/abs/1608.06993
'Paper Reading 📜 > Deep Learning' 카테고리의 다른 글
| Zero-shot, One-shot, Few-shot Learning이 무엇일까? (3) | 2023.03.12 |
|---|---|
| Prompt Engineering이 무엇일까? (0) | 2023.03.01 |
| LSTM vs GRU 뭐가 더 나을까?: Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling 논문 리뷰 (1) | 2023.01.30 |
| 알기 쉽게 LSTM networks 이해하기 (2) | 2023.01.27 |
| Distilling the Knowledge in a Neural Network 논문 리뷰 (0) | 2023.01.26 |
