Friedberg Linear Algebra
프리드버그 선형대수학을 공부하면서 각각의 장 별로 정리를 하였다.
Table of Contents
1. 벡터공간
2. 선형변환과 행렬$($This post$)$
3. 기본행렬연산과 연립일차방정식
4. 행렬식
5. 대각화
6. 내적공간
7. 표준형
The overview of this chapter
2장에서는 선형변환과 행렬의 관계$($영공간, 상공간, 선형변환의 행렬표현, 동형사상, 좌표변환$)$을 학습하였다.
2.1 선형변환, 영공간, 상공간
정의역이 $\textbf{V}$이고, 공역이 $\textbf{W}$인 함수 $\textbf{T}$를 $\textbf{T} : \textbf{V} \to \textbf{W}$라 표기한다.
정의
$\textbf{V}$와 $\textbf{W}$는 모두 $F$-벡터공간이라 하자. 모든 $x,y \in \textbf{V}, c \in F$에 대하여 다음을 모두 만족하는 함수 $\textbf{T} : \textbf{V} \to \textbf{W}$를 $\textbf{W}$로 가는 선형변환$($linear transformation$)$이라 한다.
- $\textbf{T}(x+y)=\textbf{T}(x)+\textbf{T}(y)$
- $\textbf{T}(cx)=c\textbf{T}(x)$
'$\textbf{T}$가 선형변환이다.' 라는 표현을 간단히 '$\textbf{T}$는 선형이다.' 라고 한다. $\textbf{T} : \textbf{V} \to \textbf{W}$는 다음 성질을 만족한다.
- 성질 1: $\textbf{T}$가 선형이면 $\textbf{T}(O)=O$이다.
- 성질 2: $\textbf{T}$가 선형이기 위한 필요충분조건은 모든 $x,y \in \textbf{V}, c \in F$에 대하여 $\textbf{T}(cx+y)=c\textbf{T}(x)+\textbf{T}(y)$인 것이다. 어떤 함수가 선형인지 확인할 때, 주로 사용된다.
- 성질 3: $\textbf{T}$가 선형이면 모든 $x,y \in \textbf{V}$에 대하여 $\textbf{T}(x-y)=\textbf{T}(x)-\textbf{T}(y)$이다.
- 성질 4: $\textbf{T}$가 선형이기 위한 필요충분조건은 모든 $x_1, x_2, ..., x_n \in \textbf{V}$와 $a_1, a_2, ..., a_n \in F$에 대하여 다음 식을 만족하는 것이다.
$\textbf{T}(\sum_{i=1}^{n}a_ix_i )=\sum_{i=1}^{n}a_i\textbf{T}(x_i)$
$F$-벡터공간 $\textbf{V}, \textbf{W}$에 대하여
- 항등변환 $\textbf{I_V}: \textbf{V} \to \textbf{V}$는 모든 $x \in \textbf{V}$에 대하여 $\textbf{I_V}(x)=x$라 정의되는 함수이다.
- 영변환 $\textbf{T}_0: \textbf{V} \to \textbf{W}$는 모든 $x \in \textbf{V}$에 대하여 $\textbf{T}_0(x)=O$라 정의되는 함수이다.
이를 통해 상공간과 영공간에 대해 알아보자.
정의
벡터공간 $\textbf{V}, \textbf{W}$와 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}$에 대하여
- 영공간$($null space 또는 kernel$)$은 $\textbf{T}(x)=O$인 $x \in \textbf{V}$를 원소로 가지는 집합이고, $\\textbf{N}(\textbf{T})$라 표기한다. 집합으로 나타내면 $\textbf{N}(\textbf{T})={x \in \textbf{V}: \textbf{T}(x)=O}$이다.
- 상공간$($range 또는 image$)$은 $\textbf{T}$의 함숫값을 원소로 가지는 $\textbf{W}$의 부분집합이고 $\textbf{R}(\textbf{T})$라 표기한다. 집합으로 나타내면 $\textbf{R}(\textbf{T})={\textbf{T}(x): x \in \textbf{V}}$이다.
다음의 정리는 선형변환의 상공간을 생성하는 집합을 찾는 방법이다.
정리 벡터공간 $\textbf{V}, \textbf{W}$와 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}, \textbf{V}$의 기저 $\beta={v_1,v_2,...,v_n}$에 대하여 다음이 성립한다.
$\textbf{R}(\textbf{T})=span(\textbf{T}(\beta))=span({\textbf{T}(v_1),\textbf{T}(v_2),...,\textbf{T}(v_n)})$
앞서 1장에서는 부분공간의 '크기'를 차원으로 가늠했다. 영공간과 상공간은 매우 중요하므로 차원에도 이름을 붙여 특별하게 다룬다.
벡터공간 $\textbf{V}, \textbf{W}$와 선형변환 $\textbf{T}:\textbf{V} \to \textbf{W}$에 대하여 $\textbf{N}(\textbf{T})$와 $\textbf{R}(\textbf{T})$가 유한차원이라고 가정하자.
- $\textbf{N}(\textbf{T})$의 차원을 nullity라 하고, $nullity(\textbf{T})$라 표기한다.
- $\textbf{R}(\textbf{T})$의 차원을 랭크라 하고, $rank(\textbf{T})$라 표기한다.
이를 이용해서 다음의 차원정리를 도출해낼 수 있다.
정리 - 차원정리$($dimensional theorem$)$
벡터공간 $\textbf{V}, \textbf{W}$와 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}$에 대하여 $\textbf{V}$가 유한차원이면 다음이 성립한다.
$nullity(\textbf{T})+rank(\textbf{T})=dim(\textbf{V})$
선형변환에서 단사함수$($one-to-one$)$와 전사함수$($onto$)$는 랭크, nullity와 밀접한 관련이 있다. 다음의 두 정리를 보자.
정리
벡터공간 $\textbf{V}, \textbf{W}$와 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}$에 대하여 다음이 성립한다.
$\textbf{T}$는 단사함수이다. $\Leftrightarrow $ $\textbf{N}(\textbf{T})={O}$
정리
유한차원 벡터공간 $\textbf{V}, \textbf{W}$의 차원이 같을 때, 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}$의 차원이 같을 때, 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}$에 대하여 다음 세 명제는 동치이다.
- $\textbf{T}$는 단사이다.
- $\textbf{T}$는 전사이다.
- $rank(\textbf{T})=dim(\textbf{V})$
2.2 선형변환의 행렬표현
2.1에서는 영공간과 상공간 위주로 선형변환을 다뤘다. 이제 유한차원 벡터공간을 분석하는 데 가장 중요한 '행렬을 이용한 선형변환의 표현법'을 알아보자. 이번 절에서 선형변환과 행렬이 일대일대응임을 보일 것이다. 우선 벡터공간의 순서기저 개념을 살펴보자.
정의
유한차원 벡터공간 $\textbf{V}$의 순서기저는 순서가 주어진 기저이다. 즉, 일차독립이며 $\textbf{V}$를 생성하는 벡터들로 이루어진 유한 차열을 순서기저라고 한다. 예를 들어서, $\textbf{F}^{3}$에서 $\beta={e_1,e_2,e_3}$과 $\gamma={e_2,e_1,e_3}$은 모두 순서기저이다.순서기저의 관점에서 보면 $\beta \neq \gamma$이다.
벡터공간 $\textbf{F}^{n}$에서 ${e_1,e_2,...,e_n}$을 $\textbf{F}^{n}$의 표준 순서기저라고 한다.
순서기저의 개념이 등장하였으므로 $n$차원 벡터공간의 추상적인 벡터와 $n$순서쌍을 같게 나타낼 수 있다. 이때 다음에 소개하는 좌표벡터의 개념을 사용한다.
정의
유한차원 벡터공간 $\textbf{V}$의 순서기저를 $\beta={u_1,u_2,...,u_n}$이라 하고, $x \in \textbf{V}$에 대하여 $a_1,a_2,...,a_n$은 $x = \sum_{i=1}^{n}a_iu_i$를 만족하는 유일한 스칼라라고 하자. $\beta$에 대한 $x$의 좌표벡터 $[x]_{\beta}$는 다음과 같다.
$[x]_{\beta}=\begin{pmatrix}
a_1 \\
a_2 \\
... \\
a_n
\end{pmatrix}$
위의 정의에 따르면 $[u_i]_{\beta}=e_i$이다.
정의
성분이 $A_{ij}=a_{ij}$인 $m \times n$행렬 $A$를 순서기저 $\beta$와 $\gamma$에 대한 선형변환 $\textbf{T}$의 행렬표현이라 하고 $A=[\textbf{T}]_{\beta}^{\gamma}$라 표기한다. $\textbf{V}=\textbf{W}, \beta=\gamma$이면 간단히 $A=[\textbf{T}]_{\beta}$라 표기한다.
$\textbf{T}(v_j)=\sum_{i=1}^{n}a_{ij}w_i$
이제 매우 편리한 표기법 중 하나인 크로네커 델타에 대해 소개하겠다.
정의
크로네커 델타는 다음과 같이 정의한다.
$i=j$일 때, $\delta_{ij}=1$이고, $i \neq j$일 때, $\delta_{ij}=0$
$n \times n$ 항등행렬 $I_n$의 선분은 $(I_n)_{ij}=\delta_{ij}$이다.
이제 행렬과 선형변환을 연결하였으므로 이 연결이 합과 스칼라 곱을 보존함을 보일 것이다. 이를 위하야 우선 선형변환의 합과 스칼라 곱을 정의하는 것에서 시작하자.
정의
$F$-벡터공간 $\textbf{V}, \textbf{W}$ 사이에 정의된 임의의 함수 $\textbf{T}, \textbf{U}:\textbf{V} \to \textbf{W}$와 스칼라 $a \in F$에 대하여, 두 함수의 합 $\textbf{T} + \textbf{U}: \textbf{V} \to \textbf{W}$와 스칼라 곱 $a\textbf{T}: \textbf{V} \to \textbf{W}$를 다음과 같이 정의한다.
- 합 모든 $x \in \textbf{V}$에 대하여 $(\textbf{T}+\textbf{U})(x)=\textbf{T}(x)+\textbf{U}(x)$
- 스칼라 곱 모든 $x \in \textbf{V}$에 대하여 $(a\textbf{T})(x)=a\textbf{T}(x)$
정의
$F$-벡터공간 $\textbf{V}, \textbf{W}$에 대하여 $\textbf{V}$에서 $\textbf{W}$로 가는 모든 선형변환의 모임으로 이루어진 벡터공간을 $\mathfrak{L}(\textbf{V}, \textbf{W})$라 표기한다. $\textbf{V} = \textbf{W}$이면 $\mathfrak{L}(\textbf{V}, \textbf{V})$를 간단히 $\mathfrak{L}(\textbf{V})$라 표기한다.
2.3 선형변환의 합성과 행렬 곱
2.2에서 행렬의 합과 스칼라 곱을 각각 선형변환의 합과 스칼라 곱에 대응하는 방식으로 행렬과 선형변환의 개념을 연결하였다. 선형변환의 합성에 대응하는 행렬의 연산은 무엇일까? 이것이 바로 '행렬 곱'이다. 두 선형변환 $\textbf{U}, \textbf{T}$의 합성을 나타낼 때, $\textbf{U} \circ \textbf{T}$ 대신 $\textbf{UT}$로 간단하게 표현할 것이다. 그러기 위해서 선형변환의 합성이 여전히 선형임을 보이자.
정리
$F$-벡터공간 $\textbf{V}, \textbf{W}, \textbf{Z}$와 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}, \textbf{U}: \textbf{W} \to \textbf{Z}$를 생각하자. 두 선형변환의 합성 $\textbf{UT}: \textbf{V} \to \textbf{Z}$는 선형변환이다.
선형변환의 합성에 대한 몇 가지 성질을 확인해 보자.
정리
벡터공간 $\textbf{V}$와 선형변환 $\textbf{T}, \textbf{U}_1, \textbf{U}_2 \in \mathfrak{L}(\textbf{V})$에 대하여 다음이 성립한다.
- $\textbf{T}(\textbf{U}_1 + \textbf{U}_2)=\textbf{TU}_1 + \textbf{TU}_2$이고 $(\textbf{U}_1+\textbf{U}_2)\textbf{T}=\textbf{U}_1\textbf{T}+\textbf{U}_2\textbf{T}$
- $\textbf{T}(\textbf{U}_1\textbf{U}_2) = (\textbf{TU}_1)\textbf{U}_2$
- $\textbf{TI}=\textbf{IT}=\textbf{T}$
- 모든 스칼라 $a$에 대하여 $a(\textbf{U}_1\textbf{U}_2)=(a\textbf{U}_1)\textbf{U}_2=\textbf{U}_1(a\textbf{U}_2)$
행렬 곱은 다음과 같이 정의할 수 있다.
정의
$m \times n$ 행렬 $A$와 $n \times p$ 행렬 $B$에 대하여 두 행렬 $A, B$의 곱 $AB$는 다음과 같이 정의된 $m \times p$ 행렬이다.
$1\leq i \leq m, 1\leq j\leq p$에 대하여 $(AB)_{ij}=\sum_{k=1}^{n}A_{ik}B_{kj}$
행렬 $A, B$의 크기가 서로 맞아야 행렬 곱 $AB$를 정의할 수 있다는 사실에 주의해야 한다. 다음과 같이 연상하면 쉽게 기억할 수 있다. 한 마디로 '내부'의 차원이 같아야 행렬 곱 $AB$를 정의할 수 있고, '외부'의 차원이 행렬 $AB$의 크기를 결정한다. 행렬 곱에 대한 예시는 책을 확인해보길 바란다.
$(m \times n)\dot(n \times p)=(m \times p)$
행렬 곱을 위와 같이 정의하면 다음의 정리를 이끌어낼 수 있다.
정리
유한차원 벡터공간 $\textbf{V}, \textbf{W}, \textbf{Z}$와 각각의 순서기저 $\alpha, \beta, \gamma$, 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}, \textbf{U}: \textbf{W} \to \textbf{Z}$에 대하여 다음이 성립한다.
$[\textbf{UT}]_{\alpha}^{\gamma}=[\textbf{U}]_{\beta}^{\gamma}[\textbf{T}]_{\alpha}^{\beta}$
정리
$A$가 $m \times n$ 행렬, $B$와 $C$가 $n \times p$ 행렬, $D$와 $E$가 $q \times m$ 행렬일 때, 다음이 성립한다.
- $A(B+C)=AB+AC, (D+E)A=DA+EA$
- 임의의 스칼라 $a$에 대하여 $a(AB)=(aA)B=A(aB)$
- $I_mA=A=AI_n$
정리
$\textbf{V}, \textbf{W}$는 유한차원 공간이고, 순서기저는 각각 $\beta, \gamma$이다. 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}$와 $u \in \textbf{V}$에 대하여 다음이 성립한다.
$[\textbf{T}(u)]_{\gamma}=[\textbf{T}]_{\beta}^{\gamma}[u]_{\beta}$
$m \times n$ 행렬 $A$의 좌측 곱 변환 $\textbf{L}_{A}$를 소개하며 이번 절을 마치겠다. 좌측 곱 변환은 선형변환의 성질을 바탕으로 행렬의 성질을 유추하거나, 행렬의 성질을 바탕으로 선향뱐환의 성질을 유추할 때 가장 유용하게 사용할 수 있는 도구이다. 좌측 곱 변환을 이용하면 행렬 곱에서 결합법칙이 성립함을 증명할 수 있다.
정의
$A$는 $m \times n$ 행렬이고, 성분은 체 $F$의 원소이다. 다음 선형변환을 간단히 $\textbf{L}_{A}$라 표기하자.
$\textbf{L}_{A}: \textbf{F}^{n} \to \textbf{F}^{m}, \textbf{L}_{A}(x)=Ax$
$\textbf{L}_{A}$는 좌측 곱 변환이라 한다. 이때, $x$는 $\textbf{F}^{n}$의 열벡터이고 $Ax$는 $A$와 $x$의 행렬 곱이다.
다음 정리를 통해 $\textbf{L}_{A}$가 선형이라는 사실 뿐만 아니라 유용한 성질을 많이 가지고 있음을 확인할 수 있다.
정리
$A$는 $m \times n$ 행렬이고, 성분은 체 $F$의 원소라 하자. 좌측 곱 변환 $\textbf{L}_{A}: \textbf{F}^{n} \to \textbf{F}^{m}$은 선형이다. 또한 임의의 $m \times n$ 행렬 $B$와 $\textbf{F}^{n}$의 표준 순서기저 $\beta, \textbf{F}^{m}$의 표준 순서기저 $\gamma$에 대하여 다음이 성립한다.
- $[\textbf{L}_{A}]_{\beta}^{\gamma}=A$
- $\textbf{L}_{A}=\textbf{L}_{B} \Leftrightarrow A=B$
- $\textbf{L}_{A+B}=\textbf{L}_{A}+\textbf{L}_{B}$이고, 모든 $a \in F$에 대하여 $\textbf{L}_{aA}=a\textbf{L}_{A}$이다.
- $\textbf{T}: \textbf{F}^{n} \to \textbf{F}^{m}$이 선형이면 $\textbf{T}=\textbf{L}_{C}$가 되도록 하는 $m \times n$ 행렬 $C$가 유일하게 존재한다. 실제로는 $C=[\textbf{T}]_{\beta}^{\gamma}$이다.
- $E$가 $n \times p$ 행렬이면 $\textbf{L}_{AE}=\textbf{L}_{A}\textbf{L}_{E}$이다.
- $m=n$이면 $\textbf{L}_{I_{n}}=\textbf{I}_{\textbf{F}^{n}}$이다.
좌측 곱 변환을 이용하여 행렬 곱에서 결합법칙이 성립함을 다음과 같이 보일 수 있다.
정리
$A(BC)$를 정의할 수 있는 행렬 $A, B, C$는 $(AB)C$도 정의할 수 있고 $A(BC)=(AB)C$이다. 즉, 행렬 곱에서 결합법칙이 성립한다.
2.4 가역성과 동형사상
가역성은 역함수가 존재하는가를 묻는 것이다. 이번 절에서는 선형변환의 역사상이 선형임을 보일 것이다. 이 결과는 행렬의 역행렬을 찾는 데 큰 도움이 된다. 또한 가역성과 관련된 여러 성질을 바탕으로 동형사상을 다룰 것이다. 차원이 같은 유한차원 벡터공간을 본질적으로 같다.
정의
벡터공간 $\textbf{V}, \textbf{W}$의 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}$를 생각하자. $\textbf{TU}=\textbf{I_W}$이고 $\textbf{UT}=\textbf{I_V}$인 함수 $\textbf{U}$를 $\textbf{T}$의 역함수라 한다. 역함수가 존재하는 $\textbf{T}$를 가역이라 하며 이 역함수를 $\textbf{T}^{-1}$라 표기한다. $\textbf{T}$가 가역이면 $\textbf{T}$의 역함수는 유일하다.
이때 함수가 가역이기 위한 필요충분조건은 단사이고 전사임을 기억하자.
정리
벡터공간 $\textbf{V}, \textbf{W}$와 가역인 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}$에 대하여 역함수 $\textbf{T}^{-1}: \textbf{W} \to \textbf{V}$ 또한 선형이다.
이제 행렬에 대한 내용을 살펴보자. 다음 정의는 선형변환에서 역함수를 정의한 것과 유사하다.
정의
$n \times n$ 행렬 $A$에 대하여 $AB=BA=I$인 $n \times n$ 행렬 $B$가 존재할 때, $A$는 가역이라 한다. 이때, 이 행렬 $B$를 $A$의 역행렬이라 하고, $A^{-1}$라 표기한다.
정리
유한차원 벡터공간 $\textbf{V}, \textbf{W}$와 각각의 순서기저 $\beta, \gamma$, 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}$에 대하여 $\textbf{T}$가 가역이기 위한 필요충분조건은 $[\textbf{T}]_{\beta}^{\gamma}$가 가역인 것이다. 특히, $[\textbf{T}^{-1}]_{\gamma}^{\beta}=([\textbf{T}]_{\beta}^{\gamma})^{-1}$이다.
가역성을 이용하면 이미 어렴풋이 가진 아이디어를 구체화할 수 있다. 어떤 벡터공간은 벡터의 모양이 구체적으로 다르다는 점만 제외하면 서로 매우 닮아 있다. $\textbf{M}_{2 \times 2}(F)$와 $\textbf{F}^4$에 각각 집합 $\begin{pmatrix}
a & b \\
c & d \\
\end{pmatrix}$와 4순서쌍 $(a, b, c, d)$를 대응하면 벡터의 합과 스칼라 곱이 비슷한 방식으로 작동한다. 두 벡터공간은 구조적으로 동형이다.
정의
두 벡터공간 $\textbf{V}, \textbf{W}$ 사이에 가역인 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}$가 존재하면 $\textbf{V}$는 $\textbf{W}$와 동형이다. 이때 가역인 선형변환을 $\textbf{V}$에서 $\textbf{W}$로 가는 동형사상이라 한다.
정리
같은 체 위에서 정의된 유한차원 벡터공간 $\textbf{V}, \textbf{W}$에 대하여 $\textbf{V}$가 $\textbf{W}$와 동형이기 위한 필요충분조건은 $dim(\textbf{V})=dim(\textbf{W})$이다.
추상적인 벡터공간에 정의된 선형변환과 $\textbf{F}^{n}$에서 $\textbf{F}^{m}$으로 가는 선형변환의 관계를 또렷하게 보여주는 결과를 소개하겠다.
정의
체 $F$에서의 $n$차원 벡터공간 $\textbf{V}$의 순서기저를 $\beta$라고 하자. $\beta$에 대한 $\textbf{V}$의 표준표현은 다음과 같이 정의된 함수 $\phi_{\beta}:\textbf{V} \to \textbf{F}^{n}$이다.
$x \in \textbf{V}$에 대하여 $\phi_{\beta}(x)=[x]_{\beta}$
$\phi_{\beta}$가 선형변환임을 이미 확인하였다. 다음 정리는 $\phi_{\beta}$에 대해 더 많은 정보를 제공한다.
정리
임의의 유한차원 벡터공간 $\textbf{V}$와 순서기저 $\beta$에 대하여 $\phi_{\beta}$는 동형사상이다.
이 정리에 따르면 $n$차원 벡터공간은 $\textbf{F}^{n}$과 동형이다.
차원이 각각 $n, m$인 벡터공간 $\textbf{V}, \textbf{W}$와 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}$에 대하여, $A=[\textbf{T}]_{\beta}^{\gamma}$라 하자. 이때, $\beta$와 $\gamma$는 각각 $\textbf{V}$와 $\textbf{W}$의 임의의 순서기저이다. $\phi_{\beta}$와 $\phi_{\gamma}$를 이용하면 선형변환 $\textbf{T}$와 $\textbf{L}_{A}:\textbf{F}^{n} \to \textbf{F}^{m}$ 사이의 관계를 파악할 수 있다.
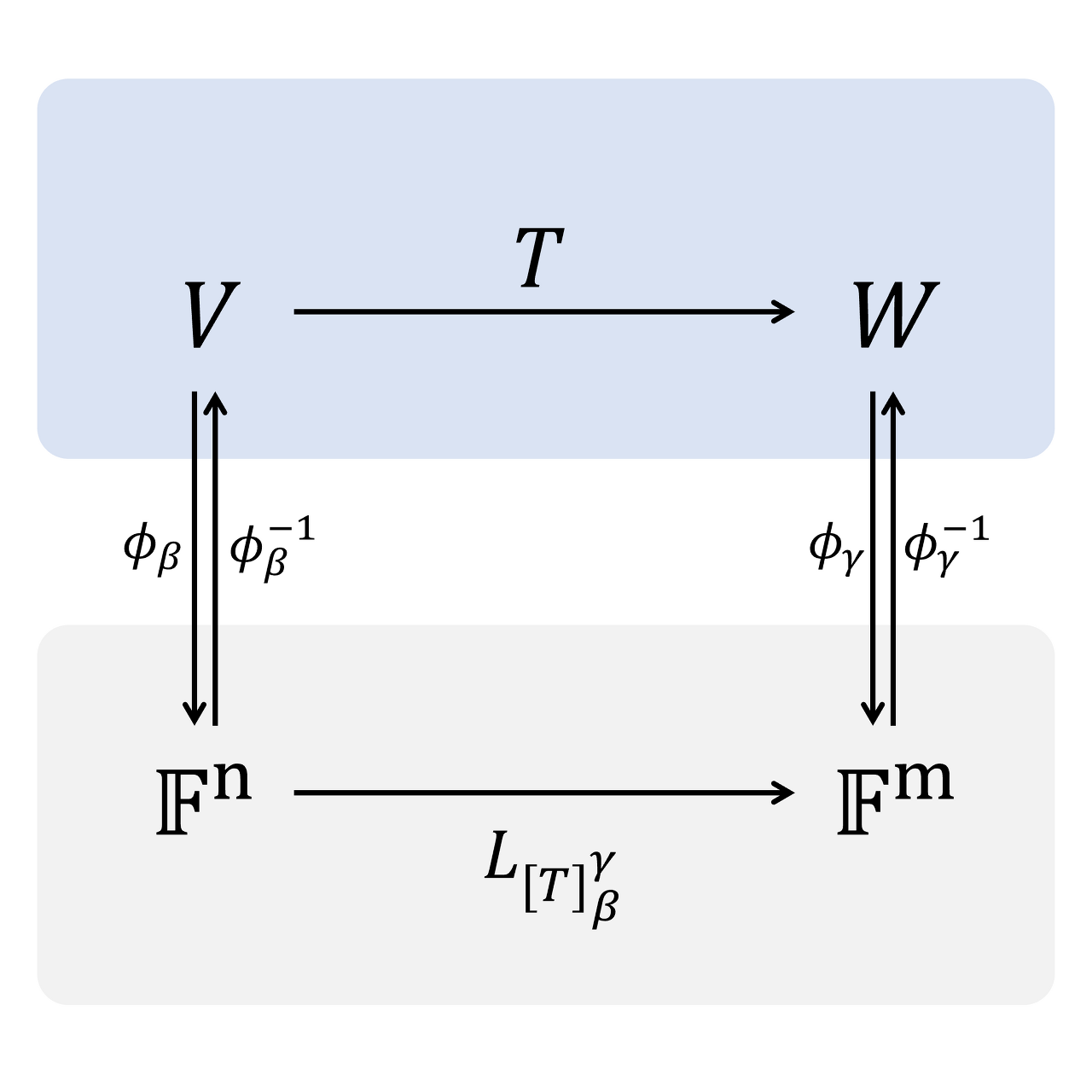
다음의 그림 1을 봐보자. $\textbf{V}$에서 $\textbf{F}^{m}$으로 가는 길은 두 가지가 있다.
- $\phi_{\beta}$를 타고 $\textbf{V}$에서 $\textbf{F}^{n}$으로 간 다음, 선형변환 $\textbf{L}_{A}$를 타고 가는 방법: $\textbf{L}_{A}\phi_{\beta}$
- $\textbf{T}$를 타고 $\textbf{V}$에서 $\textbf{W}$로 간 다음, $\phi_{\gamma}$를 타고 가는 방법: $\phi_{\gamma}\textbf{T}$
2.5 좌표변환 행렬
수학에서는 변수를 치환하면 수식이 간단해지는 경우가 많다. 이를테면 미적분학에서는 변수를 $u=x^2$으로 치환하여 $2xe^x$의 역도함수를 쉽게 구하기도 한다. 역도함수를 쉽게 구할 수 있는 간단한 형태로 바뀌기 때문이다. 다음의 변환을 생각해 보자.
$x=\frac{2}{\sqrt{5}}x^{'}-\frac{1}{\sqrt{5}}y^{'}$
$y=\frac{1}{\sqrt{5}}x^{'}+\frac{2}{\sqrt{5}}y^{'}$
방정식 $2x^2-4xy+5y^2=1$은 위의 변환을 통해 간단한 꼴인 $(x^{'})^2+6(y^{'})^2=1$로 바뀌며 자취는 타원이다. 다음 변환을 통해 평면 위의 점 $P$가 어떻게 움직이는지 기하학적으로 이해해 보자.
$\begin{pmatrix}
x \\
y
\end{pmatrix}\to \begin{pmatrix}
x^{'} \\
y^{'}
\end{pmatrix}$
처음의 $xy$좌표계가 원점에 대하여 회전한 좌표계가 $x^{'}y^{'}$좌표계이다. 새 좌표축은 타원의 축의 방향과 일치하도록 선택한다. $x^{'}$축 양의 방향과 $y^{'}$축 양의 방향 단위벡터를 모으면 다음과 같이 $\textbf{R}^2$의 순서기저가 된다.
$\beta^{'}=\left\{ \frac{1}{\sqrt{5}}\begin{pmatrix}
2 \\ 1
\end{pmatrix}, \frac{2}{\sqrt{5}}\begin{pmatrix}
-1 \\ 2
\end{pmatrix}\right\}$
주어진 좌표변환은 표준 순서기저 $\beta={e_1, e_2}$에 대한 $P$의 좌표벡터 $[P]_{\beta}=\begin{pmatrix}
x \\ y
\end{pmatrix}$를 회전하여 새롭게 얻은 기저 $\beta^{'}$에 대한 $P$의 좌표벡터 $[P]_{\beta^{'}}=\begin{pmatrix}
x^{'} \\ y^{'}
\end{pmatrix}$로 옮기는 변환이다. 이 변환에서 새로운 좌표와 기존 좌표를 연관시키는 연립방정식은 행렬을 사용하여 다음과 같이 표현할 수 있다.
$\begin{pmatrix}x \\ y\end{pmatrix}=\frac{1}{\sqrt{5}}\begin{pmatrix}
2 & -1 \\
1 & 2 \\
\end{pmatrix}\begin{pmatrix}
x^{'} \\ y^{'}
\end{pmatrix}$
이때, 행렬 $Q=\frac{1}{\sqrt{5}}\begin{pmatrix}
2 & -1 \\
1 & 2 \\
\end{pmatrix}$는 $[\textbf{I}]_{\beta^{'}}^{\beta}$과 같다. 따라서 모든 $v \in \textbf{R}^2$에 대하여 $[v]_{\beta}=Q[v]_{\beta^{'}}$이다. 일반적으로 비슷한 결과가 성립한다.
정리
유한차원 벡터공간 $\textbf{V}$의 두 순서기저 $\beta, \beta^{'}$에 대하여, $Q=[\textbf{I_V}]_{\beta^{'}}^{\beta}$라 하자. 다음이 성립한다.
- $Q$는 가역행렬이다.
- 임의의 $v \in \textbf{V}$에 대하여 $[v]_{\beta}=Q[v]_{\beta^{'}}$이다. 이렇게 정의된 행렬 $Q$를 좌표변환 행렬이라 하고, $Q$는 $\beta^{'}$좌표를 $\beta$좌표로 변환한다.
이번 절에서는 벡터공간 $\textbf{V}$에서 자기 자신으로 가는 선형변환만을 다룬다. 이런 선형변환을 $\textbf{V}$의 선형연산자라 한다.
정리
유한차원 벡터공간 $\textbf{V}$의 선형연산자 $\textbf{T}$와 $\textbf{V}$의 순서기저 $\beta, \beta^{'}$을 생각하자. $Q$가 $\beta^{'}$좌표를 $\beta$로 변환하는 행렬이라 생각하면 다음이 성립한다.
$[\textbf{T}]_{\beta^{'}}=Q^{-1}[\textbf{T}]_{\beta}Q$
따름정리
$A \in \textbf{M}_{2 \times 2}(F)$와 $\textbf{F}^{n}$의 순서기저 $\gamma$에 대하여 다음이 성립한다. 이때, $n \times n$행렬 $Q$의 $j$열은 $\gamma$의 $j$번째 벡터이다.
$[\textbf{L}_{A}]_{\gamma}=Q^{-1}AQ$
$[\textbf{L}]_{\beta^{'}}, [\textbf{L}]_{\beta}$ 사이의 관계에 이름을 붙이면 다음과 같다.
정의
$A,B$가 $\textbf{M}_{m \times m}(F)$의 행렬이라 하자. $B=Q^{-1}AQ$인 가역행렬 $Q$가 존재하면 $B$는 $A$와 서로 닮음이다. 닮음 관계는 서로 동치라고도 할 수 있다.
2.6 쌍대공간*$($선택적 학습$)$
이번 절에서는 벡터공간 $\textbf{V}$에서 체 $F$로 가는 선형변환을 집중적으로 다룬다. 이러한 선형변환을 $\textbf{V}$의 선형범함수라 한다.
정의
$F$-벡터공간 $\textbf{V}$에 대하여 벡터공간 $\mathfrak{L}(\textbf{V},F)$를 $\textbf{V}$의 쌍대공간이라 하며, 간단히 $\textbf{V}^*$라 표기한다.
$\textbf{V}^*$는 $\textbf{V}$의 모든 선형범함수로 이루어져 있으며 벡터의 합과 스칼라 곱은 2.2에서 정의한 것과 같다. $\textbf{V}$가 유한차원이면, 다음이 성립한다.
$dim(\textbf{V}^*)=dim(\mathfrak{L}(\textbf{V},F))=dim(\textbf{V})\dot dim(F)=dim(\textbf{V})$
$\textbf{V}^*$의 쌍대공간을 $\textbf{V}$의 이중 쌍대공간 $\textbf{V}^{**}$이라 정의한다.
정리
순서기저 $\beta={x_1,x_2,...,x_n}$을 가지는 유한차원 벡터공간 $\textbf{V}$와, $\beta$에 대한 $i$번째 좌표함수 $\textbf{f}_i$를 생각하자. 이때 $\beta^*={\textbf{f}_1,\textbf{f}_2,...,\textbf{f}_n}$은 $\textbf{V}^*$의 순서기저이다. 임의의 $\textbf{f} \in \textbf{V}^*$에 대하여, $\textbf{f}=\sum_{i=1}^{n}\textbf{f}(x_i)\textbf{f}_i$이다.
정의
$\textbf{f}_i(x_j)=\delta_{ij}$를 만족하는 $\textbf{V}^*$의 순서기저 $\beta^*={\textbf{f}_1, \textbf{f}_2,...,\textbf{f}_n}$을 $\beta$의 쌍대기저라고 한다.
이제 이런 의문을 가질 수 있게 된다. 행렬 $A=[\textbf{T}]_{\beta}^{\gamma}$에 대하여 행렬표현은 $A^t$이고, $\textbf{T}$와 자연스럽게 연관되는 선형변환 $\textbf{U}$가 존재할 수 있지 않을까? 여기서 배운 쌍대공간에 대한 몇 가지 사실을 적용하면 이 질문에 대한 답을 얻을 수 있다.
정리
$\textbf{V}$와 $\textbf{W}$는 $F$에서의 유한차원 벡터공간이고, 순서기저는 각각 $\beta$와 $\gamma$이다. 임의의 선형변환 $\textbf{T}:\textbf{V} \to \textbf{W}$에 대하여, 함수 $\textbf{T}^t: \textbf{W}^* \to \textbf{V}^*$를 다음과 같이 정의하자.
모든 $\textbf{g} \in \textbf{W}^*$에 대하여 $\textbf{T}^t(\textbf{g})=\textbf{g^T}$
이 함수는 선형변환이고, $[\textbf{T}^t]_{\gamma^*}^{\beta^*}=([\textbf{T}]_{\beta}^{\gamma})^t$가 성립한다.
그림 출처
그림 1: https://www.google.com/url?sa=i&url=https%3A%2F%2Faerospacekim.tistory.com%2F50&psig=AOvVaw2lIwHbsBalTCNvcj9ebfdY&ust=1672714368761000&source=images&cd=vfe&ved=0CBAQjRxqFwoTCIjm59_wp_wCFQAAAAAdAAAAABAE
'Paper Reading 📜 > Mathematics(선형대수, 확률과 통계, 미적분학)' 카테고리의 다른 글
| 프리드버그 선형대수학 - 5장 대각화 (2) | 2023.01.09 |
|---|---|
| 프리드버그 선형대수학 - 4장 행렬식 (2) | 2023.01.05 |
| 프리드버그 선형대수학 - 3장 기본행렬연산과 연립일차방정식 (2) | 2023.01.04 |
| 프리드버그 선형대수학 - 1장 벡터공간 (0) | 2022.12.30 |
| 분류성능평가지표(Precision, Recall, f1-score) (0) | 2022.12.24 |
Friedberg Linear Algebra
프리드버그 선형대수학을 공부하면서 각각의 장 별로 정리를 하였다.
Table of Contents
1. 벡터공간
2. 선형변환과 행렬$($This post$)$
3. 기본행렬연산과 연립일차방정식
4. 행렬식
5. 대각화
6. 내적공간
7. 표준형
The overview of this chapter
2장에서는 선형변환과 행렬의 관계$($영공간, 상공간, 선형변환의 행렬표현, 동형사상, 좌표변환$)$을 학습하였다.
2.1 선형변환, 영공간, 상공간
정의역이 $\textbf{V}$이고, 공역이 $\textbf{W}$인 함수 $\textbf{T}$를 $\textbf{T} : \textbf{V} \to \textbf{W}$라 표기한다.
정의
$\textbf{V}$와 $\textbf{W}$는 모두 $F$-벡터공간이라 하자. 모든 $x,y \in \textbf{V}, c \in F$에 대하여 다음을 모두 만족하는 함수 $\textbf{T} : \textbf{V} \to \textbf{W}$를 $\textbf{W}$로 가는 선형변환$($linear transformation$)$이라 한다.
- $\textbf{T}(x+y)=\textbf{T}(x)+\textbf{T}(y)$
- $\textbf{T}(cx)=c\textbf{T}(x)$
'$\textbf{T}$가 선형변환이다.' 라는 표현을 간단히 '$\textbf{T}$는 선형이다.' 라고 한다. $\textbf{T} : \textbf{V} \to \textbf{W}$는 다음 성질을 만족한다.
- 성질 1: $\textbf{T}$가 선형이면 $\textbf{T}(O)=O$이다.
- 성질 2: $\textbf{T}$가 선형이기 위한 필요충분조건은 모든 $x,y \in \textbf{V}, c \in F$에 대하여 $\textbf{T}(cx+y)=c\textbf{T}(x)+\textbf{T}(y)$인 것이다. 어떤 함수가 선형인지 확인할 때, 주로 사용된다.
- 성질 3: $\textbf{T}$가 선형이면 모든 $x,y \in \textbf{V}$에 대하여 $\textbf{T}(x-y)=\textbf{T}(x)-\textbf{T}(y)$이다.
- 성질 4: $\textbf{T}$가 선형이기 위한 필요충분조건은 모든 $x_1, x_2, ..., x_n \in \textbf{V}$와 $a_1, a_2, ..., a_n \in F$에 대하여 다음 식을 만족하는 것이다.
$\textbf{T}(\sum_{i=1}^{n}a_ix_i )=\sum_{i=1}^{n}a_i\textbf{T}(x_i)$
$F$-벡터공간 $\textbf{V}, \textbf{W}$에 대하여
- 항등변환 $\textbf{I_V}: \textbf{V} \to \textbf{V}$는 모든 $x \in \textbf{V}$에 대하여 $\textbf{I_V}(x)=x$라 정의되는 함수이다.
- 영변환 $\textbf{T}_0: \textbf{V} \to \textbf{W}$는 모든 $x \in \textbf{V}$에 대하여 $\textbf{T}_0(x)=O$라 정의되는 함수이다.
이를 통해 상공간과 영공간에 대해 알아보자.
정의
벡터공간 $\textbf{V}, \textbf{W}$와 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}$에 대하여
- 영공간$($null space 또는 kernel$)$은 $\textbf{T}(x)=O$인 $x \in \textbf{V}$를 원소로 가지는 집합이고, $\\textbf{N}(\textbf{T})$라 표기한다. 집합으로 나타내면 $\textbf{N}(\textbf{T})={x \in \textbf{V}: \textbf{T}(x)=O}$이다.
- 상공간$($range 또는 image$)$은 $\textbf{T}$의 함숫값을 원소로 가지는 $\textbf{W}$의 부분집합이고 $\textbf{R}(\textbf{T})$라 표기한다. 집합으로 나타내면 $\textbf{R}(\textbf{T})={\textbf{T}(x): x \in \textbf{V}}$이다.
다음의 정리는 선형변환의 상공간을 생성하는 집합을 찾는 방법이다.
정리 벡터공간 $\textbf{V}, \textbf{W}$와 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}, \textbf{V}$의 기저 $\beta={v_1,v_2,...,v_n}$에 대하여 다음이 성립한다.
$\textbf{R}(\textbf{T})=span(\textbf{T}(\beta))=span({\textbf{T}(v_1),\textbf{T}(v_2),...,\textbf{T}(v_n)})$
앞서 1장에서는 부분공간의 '크기'를 차원으로 가늠했다. 영공간과 상공간은 매우 중요하므로 차원에도 이름을 붙여 특별하게 다룬다.
벡터공간 $\textbf{V}, \textbf{W}$와 선형변환 $\textbf{T}:\textbf{V} \to \textbf{W}$에 대하여 $\textbf{N}(\textbf{T})$와 $\textbf{R}(\textbf{T})$가 유한차원이라고 가정하자.
- $\textbf{N}(\textbf{T})$의 차원을 nullity라 하고, $nullity(\textbf{T})$라 표기한다.
- $\textbf{R}(\textbf{T})$의 차원을 랭크라 하고, $rank(\textbf{T})$라 표기한다.
이를 이용해서 다음의 차원정리를 도출해낼 수 있다.
정리 - 차원정리$($dimensional theorem$)$
벡터공간 $\textbf{V}, \textbf{W}$와 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}$에 대하여 $\textbf{V}$가 유한차원이면 다음이 성립한다.
$nullity(\textbf{T})+rank(\textbf{T})=dim(\textbf{V})$
선형변환에서 단사함수$($one-to-one$)$와 전사함수$($onto$)$는 랭크, nullity와 밀접한 관련이 있다. 다음의 두 정리를 보자.
정리
벡터공간 $\textbf{V}, \textbf{W}$와 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}$에 대하여 다음이 성립한다.
$\textbf{T}$는 단사함수이다. $\Leftrightarrow $ $\textbf{N}(\textbf{T})={O}$
정리
유한차원 벡터공간 $\textbf{V}, \textbf{W}$의 차원이 같을 때, 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}$의 차원이 같을 때, 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}$에 대하여 다음 세 명제는 동치이다.
- $\textbf{T}$는 단사이다.
- $\textbf{T}$는 전사이다.
- $rank(\textbf{T})=dim(\textbf{V})$
2.2 선형변환의 행렬표현
2.1에서는 영공간과 상공간 위주로 선형변환을 다뤘다. 이제 유한차원 벡터공간을 분석하는 데 가장 중요한 '행렬을 이용한 선형변환의 표현법'을 알아보자. 이번 절에서 선형변환과 행렬이 일대일대응임을 보일 것이다. 우선 벡터공간의 순서기저 개념을 살펴보자.
정의
유한차원 벡터공간 $\textbf{V}$의 순서기저는 순서가 주어진 기저이다. 즉, 일차독립이며 $\textbf{V}$를 생성하는 벡터들로 이루어진 유한 차열을 순서기저라고 한다. 예를 들어서, $\textbf{F}^{3}$에서 $\beta={e_1,e_2,e_3}$과 $\gamma={e_2,e_1,e_3}$은 모두 순서기저이다.순서기저의 관점에서 보면 $\beta \neq \gamma$이다.
벡터공간 $\textbf{F}^{n}$에서 ${e_1,e_2,...,e_n}$을 $\textbf{F}^{n}$의 표준 순서기저라고 한다.
순서기저의 개념이 등장하였으므로 $n$차원 벡터공간의 추상적인 벡터와 $n$순서쌍을 같게 나타낼 수 있다. 이때 다음에 소개하는 좌표벡터의 개념을 사용한다.
정의
유한차원 벡터공간 $\textbf{V}$의 순서기저를 $\beta={u_1,u_2,...,u_n}$이라 하고, $x \in \textbf{V}$에 대하여 $a_1,a_2,...,a_n$은 $x = \sum_{i=1}^{n}a_iu_i$를 만족하는 유일한 스칼라라고 하자. $\beta$에 대한 $x$의 좌표벡터 $[x]_{\beta}$는 다음과 같다.
$[x]_{\beta}=\begin{pmatrix}
a_1 \\
a_2 \\
... \\
a_n
\end{pmatrix}$
위의 정의에 따르면 $[u_i]_{\beta}=e_i$이다.
정의
성분이 $A_{ij}=a_{ij}$인 $m \times n$행렬 $A$를 순서기저 $\beta$와 $\gamma$에 대한 선형변환 $\textbf{T}$의 행렬표현이라 하고 $A=[\textbf{T}]_{\beta}^{\gamma}$라 표기한다. $\textbf{V}=\textbf{W}, \beta=\gamma$이면 간단히 $A=[\textbf{T}]_{\beta}$라 표기한다.
$\textbf{T}(v_j)=\sum_{i=1}^{n}a_{ij}w_i$
이제 매우 편리한 표기법 중 하나인 크로네커 델타에 대해 소개하겠다.
정의
크로네커 델타는 다음과 같이 정의한다.
$i=j$일 때, $\delta_{ij}=1$이고, $i \neq j$일 때, $\delta_{ij}=0$
$n \times n$ 항등행렬 $I_n$의 선분은 $(I_n)_{ij}=\delta_{ij}$이다.
이제 행렬과 선형변환을 연결하였으므로 이 연결이 합과 스칼라 곱을 보존함을 보일 것이다. 이를 위하야 우선 선형변환의 합과 스칼라 곱을 정의하는 것에서 시작하자.
정의
$F$-벡터공간 $\textbf{V}, \textbf{W}$ 사이에 정의된 임의의 함수 $\textbf{T}, \textbf{U}:\textbf{V} \to \textbf{W}$와 스칼라 $a \in F$에 대하여, 두 함수의 합 $\textbf{T} + \textbf{U}: \textbf{V} \to \textbf{W}$와 스칼라 곱 $a\textbf{T}: \textbf{V} \to \textbf{W}$를 다음과 같이 정의한다.
- 합 모든 $x \in \textbf{V}$에 대하여 $(\textbf{T}+\textbf{U})(x)=\textbf{T}(x)+\textbf{U}(x)$
- 스칼라 곱 모든 $x \in \textbf{V}$에 대하여 $(a\textbf{T})(x)=a\textbf{T}(x)$
정의
$F$-벡터공간 $\textbf{V}, \textbf{W}$에 대하여 $\textbf{V}$에서 $\textbf{W}$로 가는 모든 선형변환의 모임으로 이루어진 벡터공간을 $\mathfrak{L}(\textbf{V}, \textbf{W})$라 표기한다. $\textbf{V} = \textbf{W}$이면 $\mathfrak{L}(\textbf{V}, \textbf{V})$를 간단히 $\mathfrak{L}(\textbf{V})$라 표기한다.
2.3 선형변환의 합성과 행렬 곱
2.2에서 행렬의 합과 스칼라 곱을 각각 선형변환의 합과 스칼라 곱에 대응하는 방식으로 행렬과 선형변환의 개념을 연결하였다. 선형변환의 합성에 대응하는 행렬의 연산은 무엇일까? 이것이 바로 '행렬 곱'이다. 두 선형변환 $\textbf{U}, \textbf{T}$의 합성을 나타낼 때, $\textbf{U} \circ \textbf{T}$ 대신 $\textbf{UT}$로 간단하게 표현할 것이다. 그러기 위해서 선형변환의 합성이 여전히 선형임을 보이자.
정리
$F$-벡터공간 $\textbf{V}, \textbf{W}, \textbf{Z}$와 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}, \textbf{U}: \textbf{W} \to \textbf{Z}$를 생각하자. 두 선형변환의 합성 $\textbf{UT}: \textbf{V} \to \textbf{Z}$는 선형변환이다.
선형변환의 합성에 대한 몇 가지 성질을 확인해 보자.
정리
벡터공간 $\textbf{V}$와 선형변환 $\textbf{T}, \textbf{U}_1, \textbf{U}_2 \in \mathfrak{L}(\textbf{V})$에 대하여 다음이 성립한다.
- $\textbf{T}(\textbf{U}_1 + \textbf{U}_2)=\textbf{TU}_1 + \textbf{TU}_2$이고 $(\textbf{U}_1+\textbf{U}_2)\textbf{T}=\textbf{U}_1\textbf{T}+\textbf{U}_2\textbf{T}$
- $\textbf{T}(\textbf{U}_1\textbf{U}_2) = (\textbf{TU}_1)\textbf{U}_2$
- $\textbf{TI}=\textbf{IT}=\textbf{T}$
- 모든 스칼라 $a$에 대하여 $a(\textbf{U}_1\textbf{U}_2)=(a\textbf{U}_1)\textbf{U}_2=\textbf{U}_1(a\textbf{U}_2)$
행렬 곱은 다음과 같이 정의할 수 있다.
정의
$m \times n$ 행렬 $A$와 $n \times p$ 행렬 $B$에 대하여 두 행렬 $A, B$의 곱 $AB$는 다음과 같이 정의된 $m \times p$ 행렬이다.
$1\leq i \leq m, 1\leq j\leq p$에 대하여 $(AB)_{ij}=\sum_{k=1}^{n}A_{ik}B_{kj}$
행렬 $A, B$의 크기가 서로 맞아야 행렬 곱 $AB$를 정의할 수 있다는 사실에 주의해야 한다. 다음과 같이 연상하면 쉽게 기억할 수 있다. 한 마디로 '내부'의 차원이 같아야 행렬 곱 $AB$를 정의할 수 있고, '외부'의 차원이 행렬 $AB$의 크기를 결정한다. 행렬 곱에 대한 예시는 책을 확인해보길 바란다.
$(m \times n)\dot(n \times p)=(m \times p)$
행렬 곱을 위와 같이 정의하면 다음의 정리를 이끌어낼 수 있다.
정리
유한차원 벡터공간 $\textbf{V}, \textbf{W}, \textbf{Z}$와 각각의 순서기저 $\alpha, \beta, \gamma$, 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}, \textbf{U}: \textbf{W} \to \textbf{Z}$에 대하여 다음이 성립한다.
$[\textbf{UT}]_{\alpha}^{\gamma}=[\textbf{U}]_{\beta}^{\gamma}[\textbf{T}]_{\alpha}^{\beta}$
정리
$A$가 $m \times n$ 행렬, $B$와 $C$가 $n \times p$ 행렬, $D$와 $E$가 $q \times m$ 행렬일 때, 다음이 성립한다.
- $A(B+C)=AB+AC, (D+E)A=DA+EA$
- 임의의 스칼라 $a$에 대하여 $a(AB)=(aA)B=A(aB)$
- $I_mA=A=AI_n$
정리
$\textbf{V}, \textbf{W}$는 유한차원 공간이고, 순서기저는 각각 $\beta, \gamma$이다. 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}$와 $u \in \textbf{V}$에 대하여 다음이 성립한다.
$[\textbf{T}(u)]_{\gamma}=[\textbf{T}]_{\beta}^{\gamma}[u]_{\beta}$
$m \times n$ 행렬 $A$의 좌측 곱 변환 $\textbf{L}_{A}$를 소개하며 이번 절을 마치겠다. 좌측 곱 변환은 선형변환의 성질을 바탕으로 행렬의 성질을 유추하거나, 행렬의 성질을 바탕으로 선향뱐환의 성질을 유추할 때 가장 유용하게 사용할 수 있는 도구이다. 좌측 곱 변환을 이용하면 행렬 곱에서 결합법칙이 성립함을 증명할 수 있다.
정의
$A$는 $m \times n$ 행렬이고, 성분은 체 $F$의 원소이다. 다음 선형변환을 간단히 $\textbf{L}_{A}$라 표기하자.
$\textbf{L}_{A}: \textbf{F}^{n} \to \textbf{F}^{m}, \textbf{L}_{A}(x)=Ax$
$\textbf{L}_{A}$는 좌측 곱 변환이라 한다. 이때, $x$는 $\textbf{F}^{n}$의 열벡터이고 $Ax$는 $A$와 $x$의 행렬 곱이다.
다음 정리를 통해 $\textbf{L}_{A}$가 선형이라는 사실 뿐만 아니라 유용한 성질을 많이 가지고 있음을 확인할 수 있다.
정리
$A$는 $m \times n$ 행렬이고, 성분은 체 $F$의 원소라 하자. 좌측 곱 변환 $\textbf{L}_{A}: \textbf{F}^{n} \to \textbf{F}^{m}$은 선형이다. 또한 임의의 $m \times n$ 행렬 $B$와 $\textbf{F}^{n}$의 표준 순서기저 $\beta, \textbf{F}^{m}$의 표준 순서기저 $\gamma$에 대하여 다음이 성립한다.
- $[\textbf{L}_{A}]_{\beta}^{\gamma}=A$
- $\textbf{L}_{A}=\textbf{L}_{B} \Leftrightarrow A=B$
- $\textbf{L}_{A+B}=\textbf{L}_{A}+\textbf{L}_{B}$이고, 모든 $a \in F$에 대하여 $\textbf{L}_{aA}=a\textbf{L}_{A}$이다.
- $\textbf{T}: \textbf{F}^{n} \to \textbf{F}^{m}$이 선형이면 $\textbf{T}=\textbf{L}_{C}$가 되도록 하는 $m \times n$ 행렬 $C$가 유일하게 존재한다. 실제로는 $C=[\textbf{T}]_{\beta}^{\gamma}$이다.
- $E$가 $n \times p$ 행렬이면 $\textbf{L}_{AE}=\textbf{L}_{A}\textbf{L}_{E}$이다.
- $m=n$이면 $\textbf{L}_{I_{n}}=\textbf{I}_{\textbf{F}^{n}}$이다.
좌측 곱 변환을 이용하여 행렬 곱에서 결합법칙이 성립함을 다음과 같이 보일 수 있다.
정리
$A(BC)$를 정의할 수 있는 행렬 $A, B, C$는 $(AB)C$도 정의할 수 있고 $A(BC)=(AB)C$이다. 즉, 행렬 곱에서 결합법칙이 성립한다.
2.4 가역성과 동형사상
가역성은 역함수가 존재하는가를 묻는 것이다. 이번 절에서는 선형변환의 역사상이 선형임을 보일 것이다. 이 결과는 행렬의 역행렬을 찾는 데 큰 도움이 된다. 또한 가역성과 관련된 여러 성질을 바탕으로 동형사상을 다룰 것이다. 차원이 같은 유한차원 벡터공간을 본질적으로 같다.
정의
벡터공간 $\textbf{V}, \textbf{W}$의 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}$를 생각하자. $\textbf{TU}=\textbf{I_W}$이고 $\textbf{UT}=\textbf{I_V}$인 함수 $\textbf{U}$를 $\textbf{T}$의 역함수라 한다. 역함수가 존재하는 $\textbf{T}$를 가역이라 하며 이 역함수를 $\textbf{T}^{-1}$라 표기한다. $\textbf{T}$가 가역이면 $\textbf{T}$의 역함수는 유일하다.
이때 함수가 가역이기 위한 필요충분조건은 단사이고 전사임을 기억하자.
정리
벡터공간 $\textbf{V}, \textbf{W}$와 가역인 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}$에 대하여 역함수 $\textbf{T}^{-1}: \textbf{W} \to \textbf{V}$ 또한 선형이다.
이제 행렬에 대한 내용을 살펴보자. 다음 정의는 선형변환에서 역함수를 정의한 것과 유사하다.
정의
$n \times n$ 행렬 $A$에 대하여 $AB=BA=I$인 $n \times n$ 행렬 $B$가 존재할 때, $A$는 가역이라 한다. 이때, 이 행렬 $B$를 $A$의 역행렬이라 하고, $A^{-1}$라 표기한다.
정리
유한차원 벡터공간 $\textbf{V}, \textbf{W}$와 각각의 순서기저 $\beta, \gamma$, 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}$에 대하여 $\textbf{T}$가 가역이기 위한 필요충분조건은 $[\textbf{T}]_{\beta}^{\gamma}$가 가역인 것이다. 특히, $[\textbf{T}^{-1}]_{\gamma}^{\beta}=([\textbf{T}]_{\beta}^{\gamma})^{-1}$이다.
가역성을 이용하면 이미 어렴풋이 가진 아이디어를 구체화할 수 있다. 어떤 벡터공간은 벡터의 모양이 구체적으로 다르다는 점만 제외하면 서로 매우 닮아 있다. $\textbf{M}_{2 \times 2}(F)$와 $\textbf{F}^4$에 각각 집합 $\begin{pmatrix}
a & b \\
c & d \\
\end{pmatrix}$와 4순서쌍 $(a, b, c, d)$를 대응하면 벡터의 합과 스칼라 곱이 비슷한 방식으로 작동한다. 두 벡터공간은 구조적으로 동형이다.
정의
두 벡터공간 $\textbf{V}, \textbf{W}$ 사이에 가역인 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}$가 존재하면 $\textbf{V}$는 $\textbf{W}$와 동형이다. 이때 가역인 선형변환을 $\textbf{V}$에서 $\textbf{W}$로 가는 동형사상이라 한다.
정리
같은 체 위에서 정의된 유한차원 벡터공간 $\textbf{V}, \textbf{W}$에 대하여 $\textbf{V}$가 $\textbf{W}$와 동형이기 위한 필요충분조건은 $dim(\textbf{V})=dim(\textbf{W})$이다.
추상적인 벡터공간에 정의된 선형변환과 $\textbf{F}^{n}$에서 $\textbf{F}^{m}$으로 가는 선형변환의 관계를 또렷하게 보여주는 결과를 소개하겠다.
정의
체 $F$에서의 $n$차원 벡터공간 $\textbf{V}$의 순서기저를 $\beta$라고 하자. $\beta$에 대한 $\textbf{V}$의 표준표현은 다음과 같이 정의된 함수 $\phi_{\beta}:\textbf{V} \to \textbf{F}^{n}$이다.
$x \in \textbf{V}$에 대하여 $\phi_{\beta}(x)=[x]_{\beta}$
$\phi_{\beta}$가 선형변환임을 이미 확인하였다. 다음 정리는 $\phi_{\beta}$에 대해 더 많은 정보를 제공한다.
정리
임의의 유한차원 벡터공간 $\textbf{V}$와 순서기저 $\beta$에 대하여 $\phi_{\beta}$는 동형사상이다.
이 정리에 따르면 $n$차원 벡터공간은 $\textbf{F}^{n}$과 동형이다.
차원이 각각 $n, m$인 벡터공간 $\textbf{V}, \textbf{W}$와 선형변환 $\textbf{T}: \textbf{V} \to \textbf{W}$에 대하여, $A=[\textbf{T}]_{\beta}^{\gamma}$라 하자. 이때, $\beta$와 $\gamma$는 각각 $\textbf{V}$와 $\textbf{W}$의 임의의 순서기저이다. $\phi_{\beta}$와 $\phi_{\gamma}$를 이용하면 선형변환 $\textbf{T}$와 $\textbf{L}_{A}:\textbf{F}^{n} \to \textbf{F}^{m}$ 사이의 관계를 파악할 수 있다.
다음의 그림 1을 봐보자. $\textbf{V}$에서 $\textbf{F}^{m}$으로 가는 길은 두 가지가 있다.
- $\phi_{\beta}$를 타고 $\textbf{V}$에서 $\textbf{F}^{n}$으로 간 다음, 선형변환 $\textbf{L}_{A}$를 타고 가는 방법: $\textbf{L}_{A}\phi_{\beta}$
- $\textbf{T}$를 타고 $\textbf{V}$에서 $\textbf{W}$로 간 다음, $\phi_{\gamma}$를 타고 가는 방법: $\phi_{\gamma}\textbf{T}$

2.5 좌표변환 행렬
수학에서는 변수를 치환하면 수식이 간단해지는 경우가 많다. 이를테면 미적분학에서는 변수를 $u=x^2$으로 치환하여 $2xe^x$의 역도함수를 쉽게 구하기도 한다. 역도함수를 쉽게 구할 수 있는 간단한 형태로 바뀌기 때문이다. 다음의 변환을 생각해 보자.
$x=\frac{2}{\sqrt{5}}x^{'}-\frac{1}{\sqrt{5}}y^{'}$
$y=\frac{1}{\sqrt{5}}x^{'}+\frac{2}{\sqrt{5}}y^{'}$
방정식 $2x^2-4xy+5y^2=1$은 위의 변환을 통해 간단한 꼴인 $(x^{'})^2+6(y^{'})^2=1$로 바뀌며 자취는 타원이다. 다음 변환을 통해 평면 위의 점 $P$가 어떻게 움직이는지 기하학적으로 이해해 보자.
$\begin{pmatrix}
x \\
y
\end{pmatrix}\to \begin{pmatrix}
x^{'} \\
y^{'}
\end{pmatrix}$
처음의 $xy$좌표계가 원점에 대하여 회전한 좌표계가 $x^{'}y^{'}$좌표계이다. 새 좌표축은 타원의 축의 방향과 일치하도록 선택한다. $x^{'}$축 양의 방향과 $y^{'}$축 양의 방향 단위벡터를 모으면 다음과 같이 $\textbf{R}^2$의 순서기저가 된다.
$\beta^{'}=\left\{ \frac{1}{\sqrt{5}}\begin{pmatrix}
2 \\ 1
\end{pmatrix}, \frac{2}{\sqrt{5}}\begin{pmatrix}
-1 \\ 2
\end{pmatrix}\right\}$
주어진 좌표변환은 표준 순서기저 $\beta={e_1, e_2}$에 대한 $P$의 좌표벡터 $[P]_{\beta}=\begin{pmatrix}
x \\ y
\end{pmatrix}$를 회전하여 새롭게 얻은 기저 $\beta^{'}$에 대한 $P$의 좌표벡터 $[P]_{\beta^{'}}=\begin{pmatrix}
x^{'} \\ y^{'}
\end{pmatrix}$로 옮기는 변환이다. 이 변환에서 새로운 좌표와 기존 좌표를 연관시키는 연립방정식은 행렬을 사용하여 다음과 같이 표현할 수 있다.
$\begin{pmatrix}x \\ y\end{pmatrix}=\frac{1}{\sqrt{5}}\begin{pmatrix}
2 & -1 \\
1 & 2 \\
\end{pmatrix}\begin{pmatrix}
x^{'} \\ y^{'}
\end{pmatrix}$
이때, 행렬 $Q=\frac{1}{\sqrt{5}}\begin{pmatrix}
2 & -1 \\
1 & 2 \\
\end{pmatrix}$는 $[\textbf{I}]_{\beta^{'}}^{\beta}$과 같다. 따라서 모든 $v \in \textbf{R}^2$에 대하여 $[v]_{\beta}=Q[v]_{\beta^{'}}$이다. 일반적으로 비슷한 결과가 성립한다.
정리
유한차원 벡터공간 $\textbf{V}$의 두 순서기저 $\beta, \beta^{'}$에 대하여, $Q=[\textbf{I_V}]_{\beta^{'}}^{\beta}$라 하자. 다음이 성립한다.
- $Q$는 가역행렬이다.
- 임의의 $v \in \textbf{V}$에 대하여 $[v]_{\beta}=Q[v]_{\beta^{'}}$이다. 이렇게 정의된 행렬 $Q$를 좌표변환 행렬이라 하고, $Q$는 $\beta^{'}$좌표를 $\beta$좌표로 변환한다.
이번 절에서는 벡터공간 $\textbf{V}$에서 자기 자신으로 가는 선형변환만을 다룬다. 이런 선형변환을 $\textbf{V}$의 선형연산자라 한다.
정리
유한차원 벡터공간 $\textbf{V}$의 선형연산자 $\textbf{T}$와 $\textbf{V}$의 순서기저 $\beta, \beta^{'}$을 생각하자. $Q$가 $\beta^{'}$좌표를 $\beta$로 변환하는 행렬이라 생각하면 다음이 성립한다.
$[\textbf{T}]_{\beta^{'}}=Q^{-1}[\textbf{T}]_{\beta}Q$
따름정리
$A \in \textbf{M}_{2 \times 2}(F)$와 $\textbf{F}^{n}$의 순서기저 $\gamma$에 대하여 다음이 성립한다. 이때, $n \times n$행렬 $Q$의 $j$열은 $\gamma$의 $j$번째 벡터이다.
$[\textbf{L}_{A}]_{\gamma}=Q^{-1}AQ$
$[\textbf{L}]_{\beta^{'}}, [\textbf{L}]_{\beta}$ 사이의 관계에 이름을 붙이면 다음과 같다.
정의
$A,B$가 $\textbf{M}_{m \times m}(F)$의 행렬이라 하자. $B=Q^{-1}AQ$인 가역행렬 $Q$가 존재하면 $B$는 $A$와 서로 닮음이다. 닮음 관계는 서로 동치라고도 할 수 있다.
2.6 쌍대공간*$($선택적 학습$)$
이번 절에서는 벡터공간 $\textbf{V}$에서 체 $F$로 가는 선형변환을 집중적으로 다룬다. 이러한 선형변환을 $\textbf{V}$의 선형범함수라 한다.
정의
$F$-벡터공간 $\textbf{V}$에 대하여 벡터공간 $\mathfrak{L}(\textbf{V},F)$를 $\textbf{V}$의 쌍대공간이라 하며, 간단히 $\textbf{V}^*$라 표기한다.
$\textbf{V}^*$는 $\textbf{V}$의 모든 선형범함수로 이루어져 있으며 벡터의 합과 스칼라 곱은 2.2에서 정의한 것과 같다. $\textbf{V}$가 유한차원이면, 다음이 성립한다.
$dim(\textbf{V}^*)=dim(\mathfrak{L}(\textbf{V},F))=dim(\textbf{V})\dot dim(F)=dim(\textbf{V})$
$\textbf{V}^*$의 쌍대공간을 $\textbf{V}$의 이중 쌍대공간 $\textbf{V}^{**}$이라 정의한다.
정리
순서기저 $\beta={x_1,x_2,...,x_n}$을 가지는 유한차원 벡터공간 $\textbf{V}$와, $\beta$에 대한 $i$번째 좌표함수 $\textbf{f}_i$를 생각하자. 이때 $\beta^*={\textbf{f}_1,\textbf{f}_2,...,\textbf{f}_n}$은 $\textbf{V}^*$의 순서기저이다. 임의의 $\textbf{f} \in \textbf{V}^*$에 대하여, $\textbf{f}=\sum_{i=1}^{n}\textbf{f}(x_i)\textbf{f}_i$이다.
정의
$\textbf{f}_i(x_j)=\delta_{ij}$를 만족하는 $\textbf{V}^*$의 순서기저 $\beta^*={\textbf{f}_1, \textbf{f}_2,...,\textbf{f}_n}$을 $\beta$의 쌍대기저라고 한다.
이제 이런 의문을 가질 수 있게 된다. 행렬 $A=[\textbf{T}]_{\beta}^{\gamma}$에 대하여 행렬표현은 $A^t$이고, $\textbf{T}$와 자연스럽게 연관되는 선형변환 $\textbf{U}$가 존재할 수 있지 않을까? 여기서 배운 쌍대공간에 대한 몇 가지 사실을 적용하면 이 질문에 대한 답을 얻을 수 있다.
정리
$\textbf{V}$와 $\textbf{W}$는 $F$에서의 유한차원 벡터공간이고, 순서기저는 각각 $\beta$와 $\gamma$이다. 임의의 선형변환 $\textbf{T}:\textbf{V} \to \textbf{W}$에 대하여, 함수 $\textbf{T}^t: \textbf{W}^* \to \textbf{V}^*$를 다음과 같이 정의하자.
모든 $\textbf{g} \in \textbf{W}^*$에 대하여 $\textbf{T}^t(\textbf{g})=\textbf{g^T}$
이 함수는 선형변환이고, $[\textbf{T}^t]_{\gamma^*}^{\beta^*}=([\textbf{T}]_{\beta}^{\gamma})^t$가 성립한다.
그림 출처
그림 1: https://www.google.com/url?sa=i&url=https%3A%2F%2Faerospacekim.tistory.com%2F50&psig=AOvVaw2lIwHbsBalTCNvcj9ebfdY&ust=1672714368761000&source=images&cd=vfe&ved=0CBAQjRxqFwoTCIjm59_wp_wCFQAAAAAdAAAAABAE
'Paper Reading 📜 > Mathematics(선형대수, 확률과 통계, 미적분학)' 카테고리의 다른 글
| 프리드버그 선형대수학 - 5장 대각화 (2) | 2023.01.09 |
|---|---|
| 프리드버그 선형대수학 - 4장 행렬식 (2) | 2023.01.05 |
| 프리드버그 선형대수학 - 3장 기본행렬연산과 연립일차방정식 (2) | 2023.01.04 |
| 프리드버그 선형대수학 - 1장 벡터공간 (0) | 2022.12.30 |
| 분류성능평가지표(Precision, Recall, f1-score) (0) | 2022.12.24 |
